
Week Five: Multiple Linear Regression
Welcome!
In this week’s coursework we are going to build off the concepts we learned last week and delve deeper into linear regression. We are going to explore multiple linear regression, a statistical model where we have multiple explanatory variables and a single numerical response. We are going to refresh how to visualize these types of models, practice fitting these types of models in R, and the learn how to interpret these types of models.
0.1 Learning Outcomes
By the end of this coursework you should be able to:
- describe to someone what a multiple linear regression is
- outline how a categorical explanatory variable can be included in a simple linear regression
- visualize multiple linear regression models with one numerical and one categorical explanatory variable
- calculate the simple linear regression line for each group of a categorical variable
- outline how a second numerical explanatory variable can be included in a simple linear regression
- visualize multiple linear regression models with two numerical explanatory variables
- interpret the coefficient of each explanatory variable included in the regression model
- recite different methods that can be used to decide what multiple linear regression model is “best”
- describe the benefits and costs of using “model selection” for deciding on a multiple linear regression model
1 Prepare
1.1 Textbook Reading
Reading Guide – Due Monday by the start of class
1.2 Concept Quiz – Due Monday by the start of class
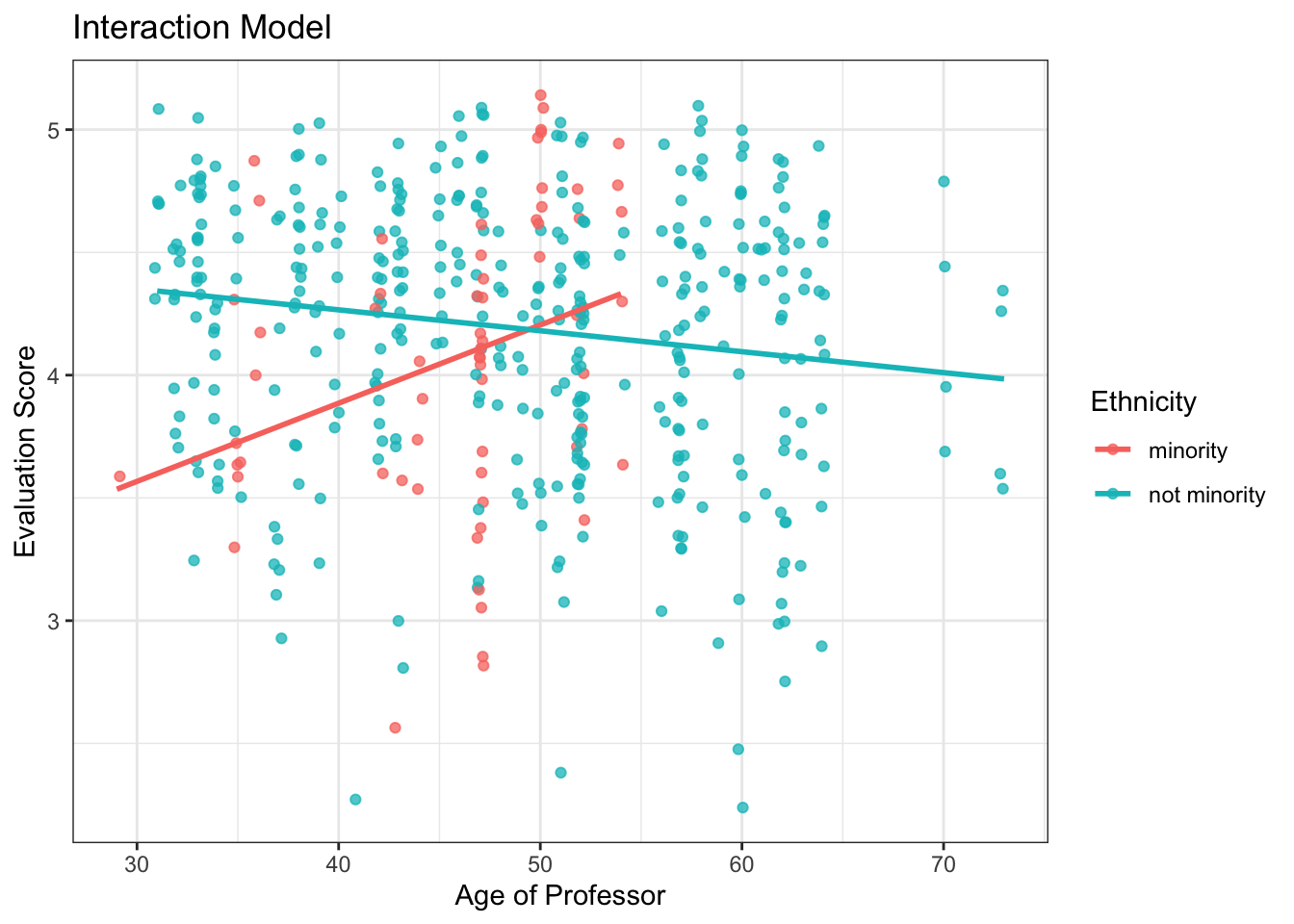
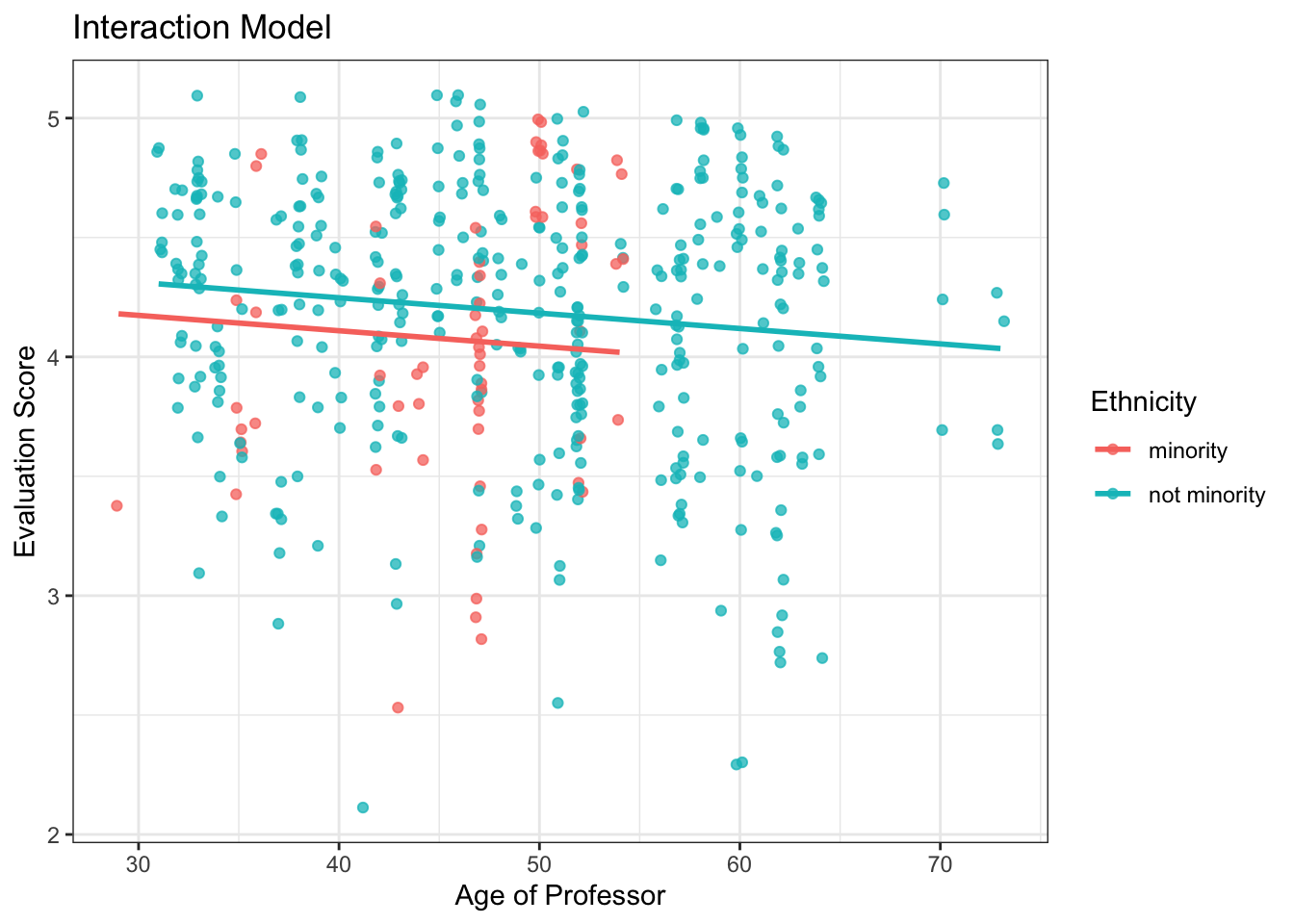
Question 1 – Based on the visualizations above, I believe the [interaction / parallel slopes] model is more appropriate because the slopes between the groups are [very different / very similar].
Question 2 – What type of model does the following code obtain?
minority_lm <- lm(score ~ age * ethnicity, data = evals)- interaction model
- parallel slopes model
- simple linear regression model
The following is the output from the above regression model (from Question 2):
# A tibble: 4 × 7
term estimate std_error statistic p_value lower_ci upper_ci
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 intercept 2.61 0.518 5.04 0 1.59 3.63
2 age 0.032 0.011 2.84 0.005 0.01 0.054
3 ethnicity: not minority 2.00 0.534 3.74 0 0.945 3.04
4 age:ethnicitynot minor… -0.04 0.012 -3.51 0 -0.063 -0.018Question 3 – The intercept line represents the [evaluation score / mean evaluation score] for [male / female / minority / non-minority] faculty.
Question 4 – The age line represents the relationship between age and evaluation scores for [male / female / minority / non-minority] faculty.
Question 5 – The ethnicity:not minority line represents the [mean / adjustment to the mean] evaluation score for [male / female / minority / non-minority] faculty.
Question 6 – The age:ethnicitynot minority line represents the [slope / adjustment to the slope] for the relationship between age and evaluation scores for [male / female / minority / non-minority] faculty.
Question 7 – The value of the age:ethnicitynot minority line (-0.004) [does / does not ] match the decision I made in Question 1 as there is [little difference / substantial difference] in the slopes between the minority and non-minority faculty.
Question 8 – What type of model does the following code obtain?
bty_lm <- lm(score ~ age + bty_avg, data = evals)- multiple linear regression with two numerical predictors
- interaction model
- parallel slopes
The following is the output from the above regression model (from Question 8):
# A tibble: 3 × 7
term estimate std_error statistic p_value lower_ci upper_ci
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 intercept 4.06 0.17 23.9 0 3.72 4.39
2 age -0.003 0.003 -1.15 0.251 -0.008 0.002
3 bty_avg 0.061 0.017 3.55 0 0.027 0.094Question 9 – The intercept represents the [course evaluation score / mean course evaluation score] for professors whose age is __ and who have a average beauty score of ___.
Question 10 – We interpret the value of -0.003 by age as:
For every [1 day / 1 year / 1 evaluation] increase in professor’s [evaluation score / age / average beauty] we expect the [course evaluation score / mean course evaluation score] to [increase / decrease] by __, after accounting for [ethnicity / gender / average beauty scores].
