Distributions and Simulation

Welcome to the final week of content! This week you will learn about simulating data in R. By the end of the week you should:

📽 Watch Videos: 17 minutes

📖 Readings: 15-20 minutes

✅ Preview Activities: 1

In statistics, we often want to simulate data (or create fake data) for a variety of purposes. For example, in your first statistics course, you may have flipped coins to “simulate” a 50-50 chance. This week, we will learn how to simulate data from statistical distributions using R.

1 Simulation in R

📖 Required Reading: R Programming for Data Science : Simulation

✅ : Check-in 9.1: Distributions & Simulation

Question 1: What does the output of pnorm(-4, mean = 2, sd = 4) mean?

Tip

Drawing pictures of the relevant distribution may help.

Question 2: Why does rnorm(mean = 0, sd = 1) give an error?

Question 3: What does map(-2:2, rnorm, n = 5) do?

Question 4: Why does map_chr(-2:2, rnorm, n = 5) result in an error?

Question 5: The output of map(1:5, runif) is a [vector  list] with ___ elements. The third element is a [vector / list] with ___ random draw(s) from a Uniform distribution with min = ___ and max = ___.

Setting a Random Number Seed

Functions like rnorm() rely on something called pseudo-randomness. Because computers can never be truly random, complicated processes are implemented to make “random” number generation be so unpredictable as to behave like true randomness.

This means that projects involving simulation are harder to make reproducible. For example, here are two identical lines of code that give different results!

rnorm(1, mean = 0, sd = 1)
[1] 0.01986493
rnorm(1, mean = 0, sd = 1)
[1] 0.7857989

Fortunately, pseudo-randomness depends on a seed, which is an arbitrary number where the randomizing process starts. Normally, R will choose the seed for you, from a pre-generated vector:

head(.Random.seed)
[1]       10403           4 -1115758636  1640221399    59814093   165234788

However, you can also choose your own seed using the set.seed() function. This guarantees your results will be consistent across runs (and hopefully computers):

set.seed(1234)

rnorm(1, mean = 0, sd = 1)
[1] -1.207066
set.seed(1234)

rnorm(1, mean = 0, sd = 1)
[1] -1.207066

Of course, it doesn’t mean the results will be the same in every subsequent run if you forget or reset the seed in between each line of code!

set.seed(1234)

rnorm(1, mean = 0, sd = 1)
[1] -1.207066
## Calling rnorm() again without a seed "resets" the seed! 
rnorm(1, mean = 0, sd = 1)
[1] 0.2774292

It is very important to always set a seed at the beginning of a Quarto document that contains any random steps, so that your rendered results are consistent.

Caution

Note, though, that this only guarantees your rendered results will be the same if the code has not changed.

Changing any part of the code will re-randomize everything that comes after it!

When writing up a report which includes results from a random generation process, in order to ensure reproducibility in your document, use `{r}` or `r` to include your output within your written description with inline code.

Reproducibility: inline code example 
my_rand <- rnorm(1, mean = 0, sd = 1)
my_rand
[1] 1.084441

Using `r my_rand` will display the result within my text:

My random number is 1.0844412.

Alternatively, you could have put the rnorm code directly into the inline text `r rnorm(1, mean = 0, sd = 1)`, but this can get messy if you have a result that requires a larger chunk of code.

2 Plotting Distributions

Here is the code is what I made to create the density plot from the lecture video:

First, I created a tibble of 100 heights randomly simulated (read drawn) from a normal distribution with a mean of 67 and standard deviation of 3.

set.seed(93401)
my_samples <- tibble(height = rnorm(n    = 100, 
                                    mean = 67, 
                                    sd   = 3)
                     )

my_samples |> 
  head()
# A tibble: 6 × 1
  height
   <dbl>
1   63.1
2   66.7
3   68.2
4   63.4
5   68.9
6   71.4

To visualize the simulated heights, we can look at the density of the values. We plot the simulated values using geom_histogram() and define a local aesthetic to calculate and plot the density of these values.

my_samples %>%
  ggplot(aes(x = height)) +
  geom_histogram(aes(y = ..density..), 
                 binwidth = 1.75, fill = "grey") +
  stat_function(fun = ~ dnorm(., mean = 67, sd = 3), 
                col = "cornflowerblue", lwd = 2) + 
  xlim(c(55, 80))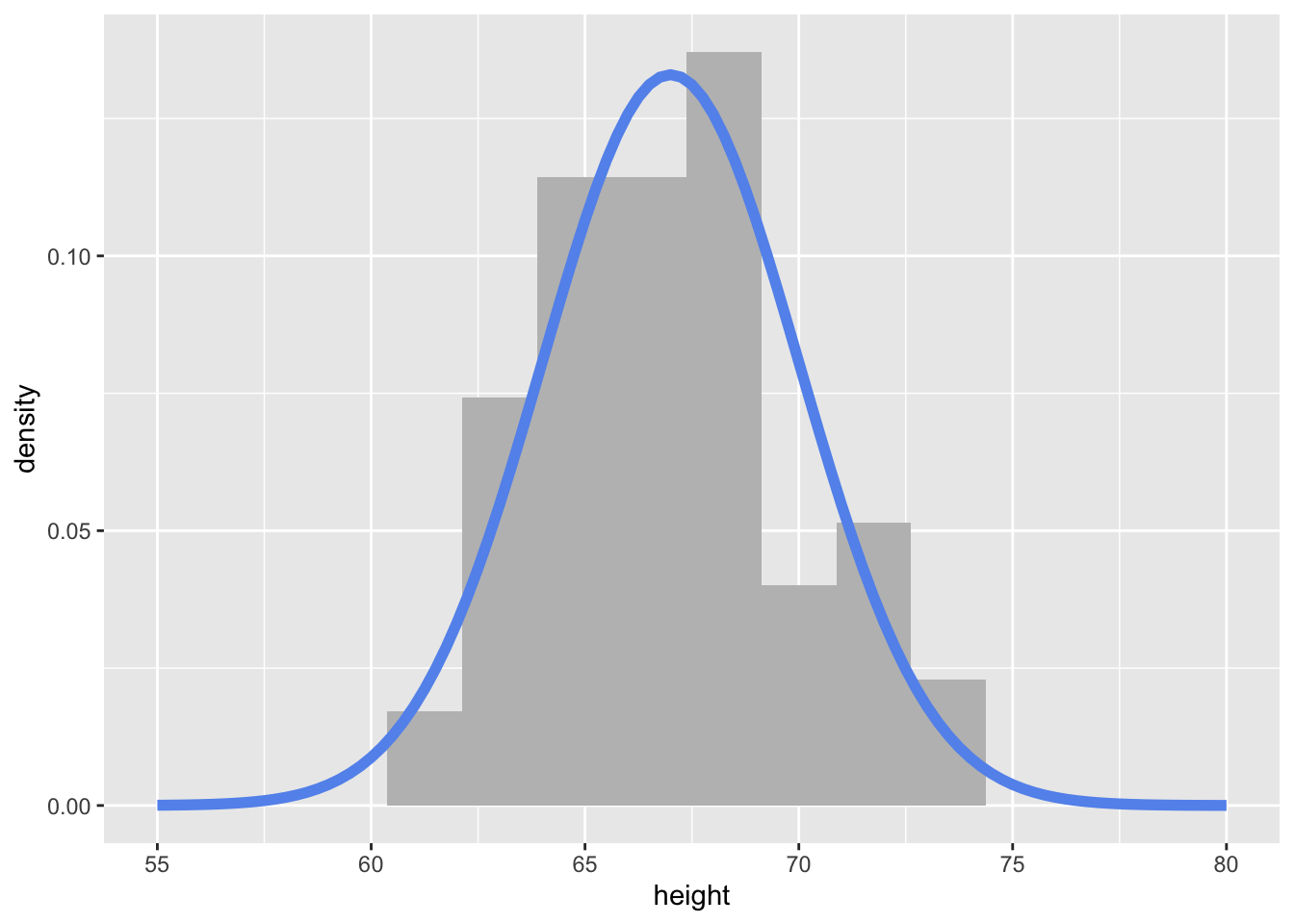

Adding a distribution to a plot

Notice how I’m using stat_function() to add a specific function to the plot. Here, I’m using the dnorm() function, with a specified mean and sd.