Confidence Intervals – Real Life Sampling Distributions

Course Updates

  • Lab 4 revisions are due on Friday (May 16)
  • Lab 3 second revisions are due on Friday (May 16)
  • Midterm Projects will be graded by Sunday (May 18)

Don’t forget reflections!

If your reflections are not present by the deadline for revisions, your revisions are not eligible to be regraded. Please don’t forget your reflections!

What if I only have one sample?

Approximate the variability you’d expect to see in other samples!

Bootstrapping!

A Bootstrap Resample

  • Assumes the original sample is “representative” of observations in the population.
  • Uses the original sample to generate new samples that might have occurred with additional sampling.


We can use the statistics from these bootstrap resamples to approximate the true sampling distribution!

Why do we want a sampling distribution?

Estimating a population parameter

  • We are interested in knowing how a statistic varies from sample to sample.
  • Knowing a statistic’s behavior helps us make better / more informed decisions!
  • This helps us estimate what values are more or less likely for the population parameter to have.

Confidence Intervals

Capture a range of plausible values for the population parameter.


Are more likely to capture the population parameter than a point estimate.

How do I get this plausible range of values?

Bootstrapping!

  1. From your original sample, resample with replacement the same number of times as your original sample.

This is your bootstrap resample.

  1. Repeat this process many, many times.
  1. Calculate a numerical summary (e.g., mean, median) for each bootstrap resample.

These are your bootstrap statistics

Bootstrap Distribution

a distribution of the bootstrap statistics from every bootstrap resample


Displays the variability in the statistic that could have happened with repeated sampling.

Approximates the true sampling distribution!

Penguins!

A picture of an Adelie penguin. An adult Adelie penguin is black on the head, throat and upper parts, with snowy white underparts. The penguin has a conspicuous white eye ring around a black iris. Its beak is largely covered with black feathers, leaving only the tip exposed; this is primarily black, though it can show indistinct reddish-brown markings. The upper surface of the wing is black with a white trailing edge, while the underside is white with a narrow black leading edge and a small black tip. The legs and feet, which are mostly unfeathered, are pinkish.

A picture of a Chinstrap penguin. An adult Chinstrap penguin has flippers that are black with a white edge; the inner sides of the flippers are white. A Chinstrap penguin's face is white extending behind the eyes, which are reddish brown; the chin and throat are white, as well, while the short bill is black. Chinstrap penguins have strong legs and the webbed feet that are pink. 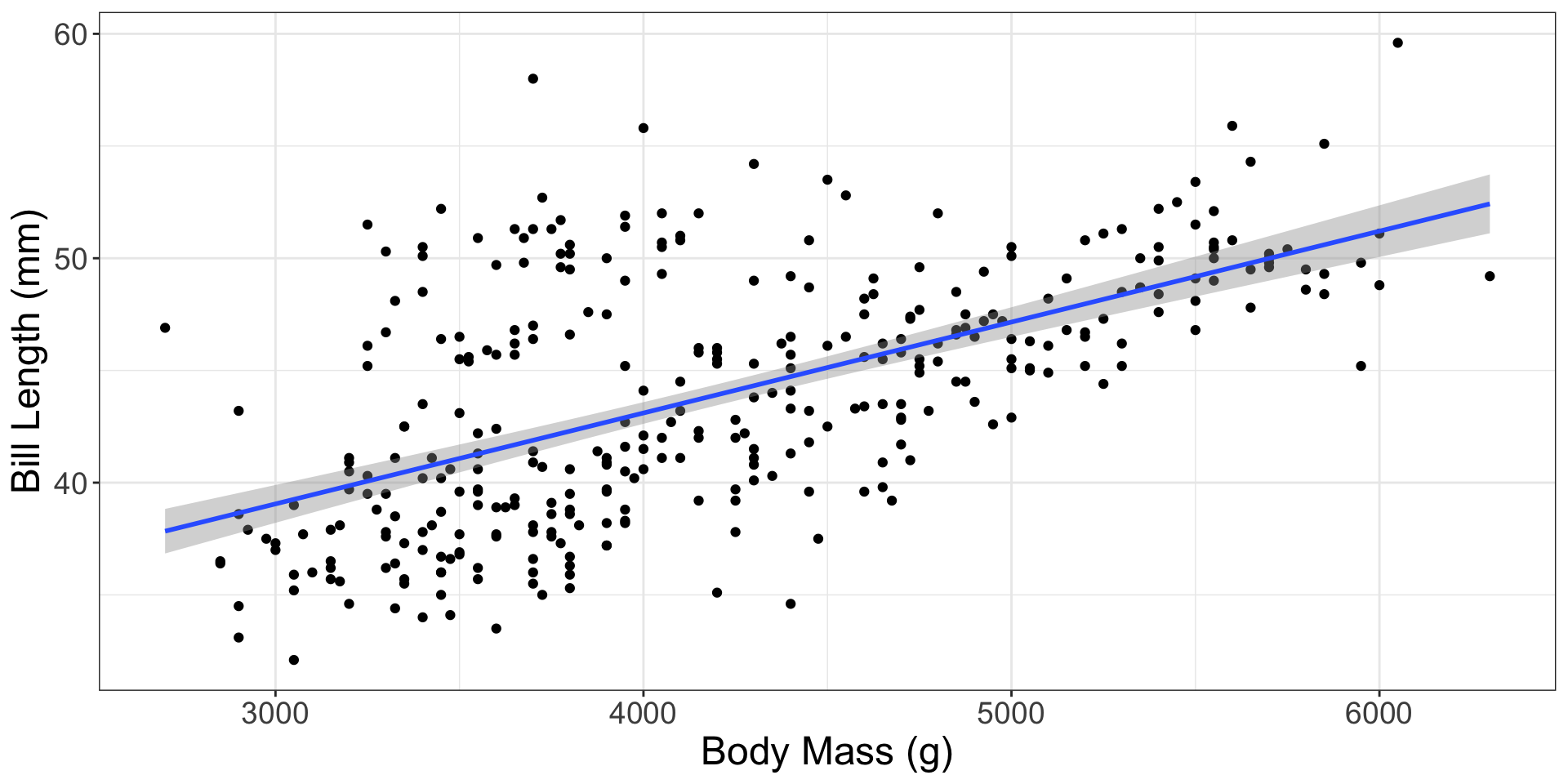Its short, stumpy legs give it a distinct waddle when it walks.

Statistic: \(\beta_1\)

The relationship between penguin’s bill length and body mass for all penguins in the Palmer Archipelago

In this sample of 344 penguins…

\[\widehat{\text{bill length}} = 26.899 + 0.004 \times \text{body mass}\]


What slope could have happened in a different sample of penguins?

Generating bootstrap resamples and calculating bootstrap statistics


Step 1: specify() your response and explanatory variables

Step 2: generate() bootstrap resamples

Step 3: calculate() the statistic of interest

Step 1: Specify your variables!

penguins %>% 
  specify(response = bill_length_mm, 
          explanatory = body_mass_g)

Step 2: Generate your resamples!

penguins %>% 
  specify(response = bill_length_mm, 
          explanatory = body_mass_g) %>% 
  generate(reps = 500, type = "bootstrap")


reps – the number of resamples you want to generate


"bootstrap" – the method that should be used to generate the new samples

Your turn!


Why do we resample with replacement when creating a bootstrap distribution?


When we resample with replacement from our original sample what are we assuming about the original sample?

Step 3: Calculate your statistics!

penguins %>% 
  specify(response = bill_length_mm, 
          explanatory = body_mass_g) %>% 
  generate(reps = 1000, 
           type = "bootstrap") %>% 
  calculate(stat = "slope")


"slope" – the statistic of interest

The final product

visualize(boot1) + 
  labs(title = "Distribution of 1,000 Bootstrap Resamples", 
       x = "Slope Statistic", 
       y = "")

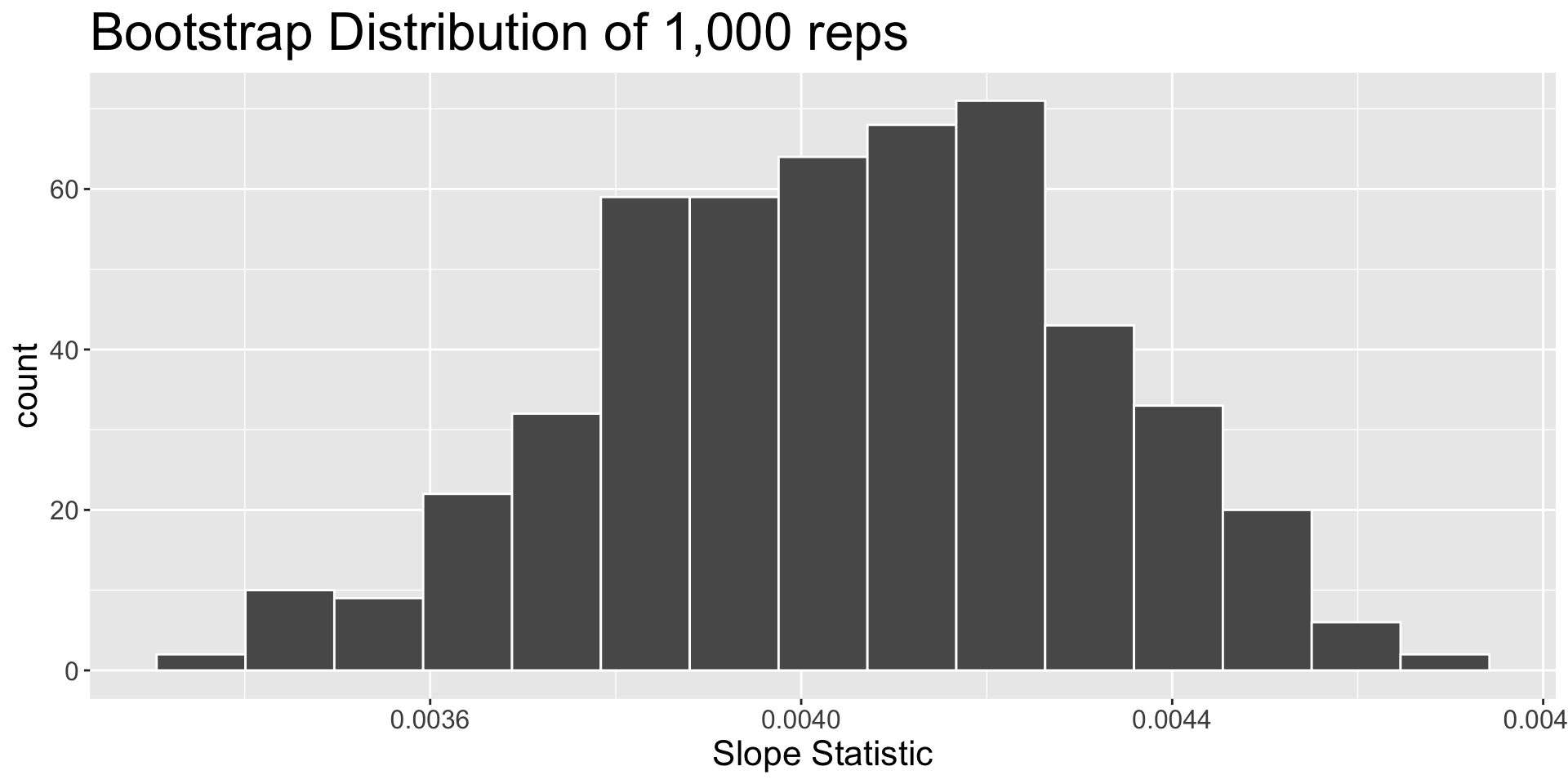
A plausible range of values for \(\beta_1\)

visualise(boot1) +
  shade_confidence_interval(endpoints = boot1_CI, 
                            color = "red", 
                            fill = "pink") +  
  labs(title = "Distribution of 1,000 Bootstrap Resamples", 
       x = "Slope Statistic", 
       y = "")

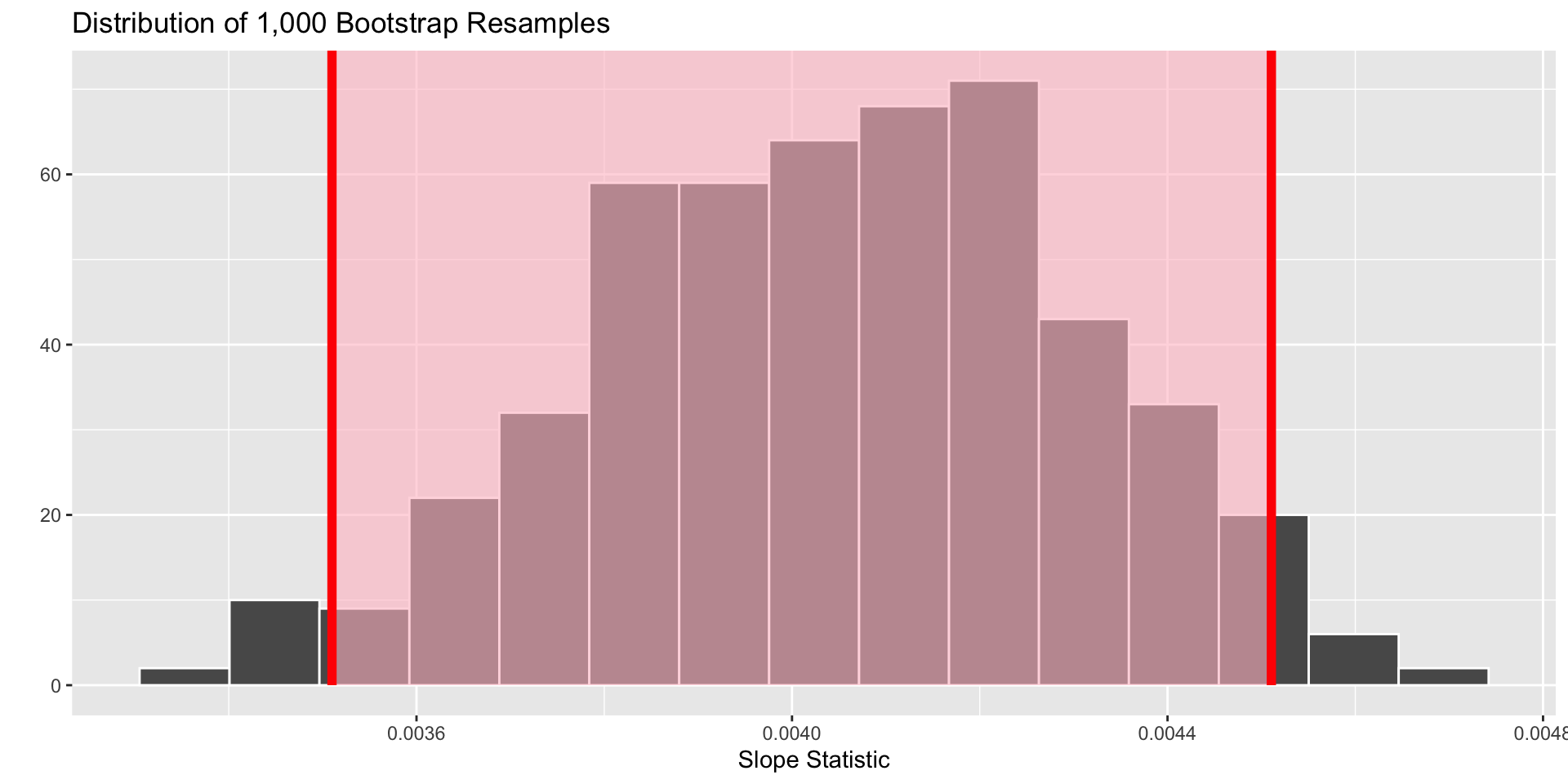
The 95% confidence interval is…

get_confidence_interval(boot1, 
                        level = 0.95, 
                        type = "percentile")


Lower Bound Upper Bound
0.00351 0.00451

What do we hope is captured by this interval?

How do we interpret this interval?

“We are 95% confident the slope of the relationship between bill length and body mass for all Adelie, Chinstrap, and Gentoo penguins in the Palmer Archipelago is between 0.00355 and 0.00453.


“For every 1000 gram (~2.2lbs) increase in a penguin’s body mass, we are 95% confident the length of an Adelie, Chinstrap, or Gentoo penguins’s bill will increase between 3.55 and 4.53mm.

Classic interpretation mistakes


“There is a 95% probability that \(\beta_1\) is between 0.00355 and 0.00453.”


“We are 95% confident the sample statistic is in our interval.”

Scaling to Multiple Linear Regression

How does the relationship between bill length and body mass change based on a penguin’s sex?

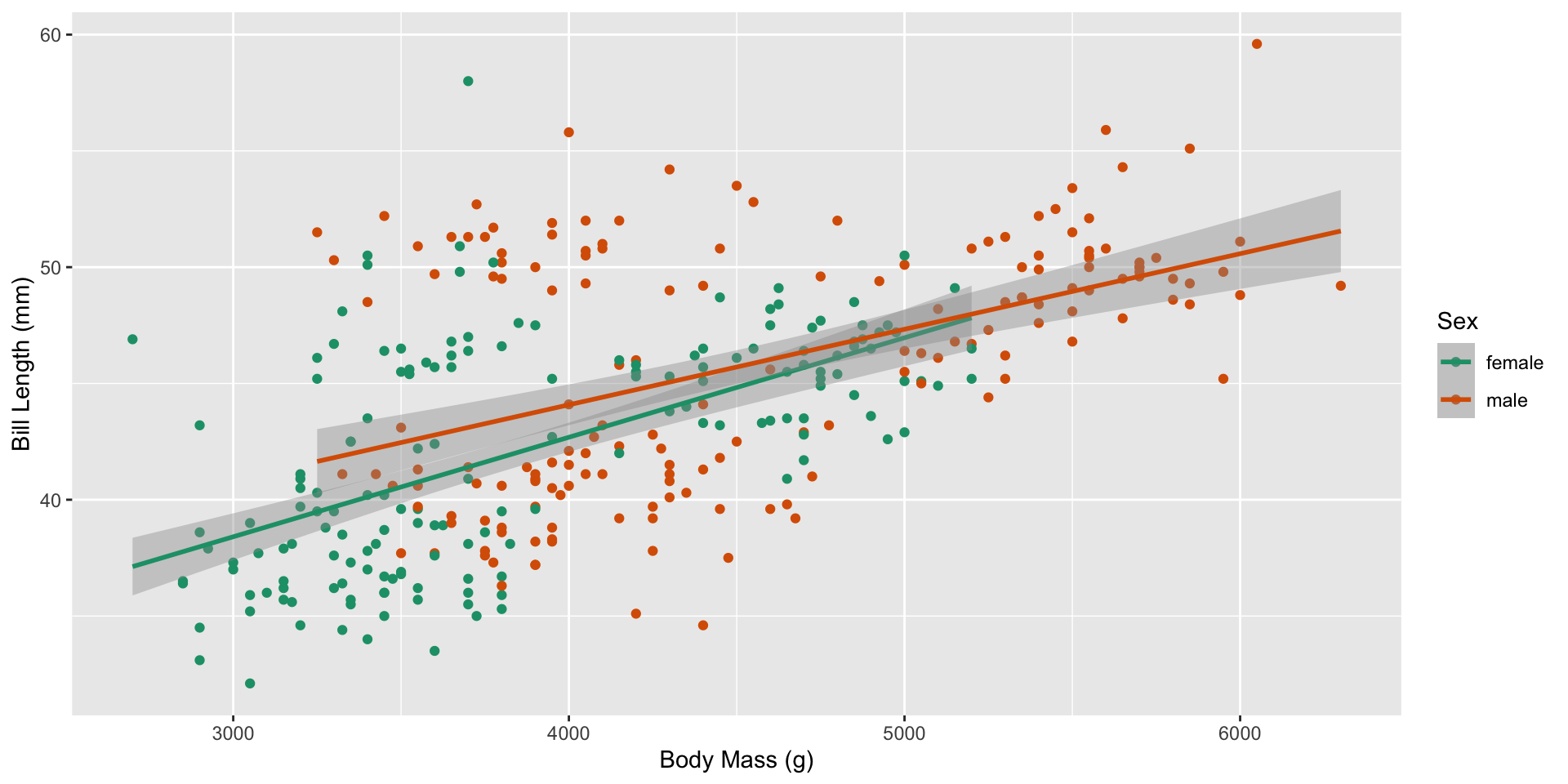
What changes?

The original sample of 344 penguins were broken down into the following groups (plus 11 NA values):

Sex Sample Size
female 165
male 168

Before we resampled with replacement 344 times.

If we resample with replacement 333 times, are we guaranteed to get 165 female penguins and 168 male penguins in each sample?

Getting our Observed Statistic

Step 1: Fitting our Model

observed_fit <- penguins %>%
  specify(bill_length_mm ~ body_mass_g * sex) %>%
  fit()

Syntax changes

When we have multiple explanatory variables, we need to use the “tilde” (~) syntax to specify our model. We also use the fit() function instead of the calculate() function.

Getting our Observed Statistic

Step 2: Finding our Statistic

term estimate
intercept 25.5713814
body_mass_g 0.0042787
sexmale 5.5160611
body_mass_g:sexmale -0.0010301

Which statistic measures how different the slopes are between male and female penguins?

Generating Bootstrap Fits

bootstrap_fits <- penguins %>%
  specify(bill_length_mm ~ body_mass_g * sex) %>%
  generate(reps = 1000, type = "bootstrap") %>%
  fit()

Obtaining a Bootstrap Confidence Interval

get_confidence_interval(bootstrap_fits,
                        point_estimate = observed_fit,
                        level = 0.90, 
                        type = "percentile")
# A tibble: 4 × 3
  term                lower_ci  upper_ci
  <chr>                  <dbl>     <dbl>
1 body_mass_g          0.00365  0.00489 
2 body_mass_g:sexmale -0.00198 -0.000118
3 intercept           23.0     28.4     
4 sexmale              1.23     9.88

How do we interpret this interval?

Lower Bound Upper Bound
-0.0019812 -0.0001181

We are 90% confident that the for every 1,000 gram increase in a penguin’s body mass (~2.2lbs), the length of a male penguin’s bill is between 0.118 and 1.98mm shorter than a female penguin’s bill.

To Do List by Wednesday

  • Hypothesis test reading guide
  • Hypothesis test concept quiz
  • Confidence interval R tutorial
  • Hypothesis test R tutorial