Simulating Probabilities & Datasets

Today we will…

  • Reminder about Lab 8 (and 9 and 10) Code Review
  • Thinking through a probability simulation task
  • Introduce Lab 9
    • Refresher on linear regression
    • Tools for extracting elements from a regression
  • Survey on Experiences in STAT 331 / 531
  • Work time!

Don’t forget to complete your Lab 8 code review!

Don’t forget to complete your Lab 8 code review!


Make sure your feedback follows the code review guidelines.

Insert your review into the comment box!

Lab 9: Simulating Probabilities

The Birthday Problem

Simulate the approximate probability that at least two people have the same birthday (same day of the year, not considering year of birth or leap years).

Writing a function to…

  • simulate the birthdays of 50 people.
  • count how many birthdays are shared.
  • return whether or not a shared birthday exists.

Step 1 – simulate the birthdays of 50 people

get_shared_birthdays <- function(n = 50){
  
  bday_data <- tibble(person = 1:n,
                      bday   = sample(1:365, 
                                      size = n, 
                                      replace = TRUE)
                      )
}

Why did I set replace = TRUE for the sample() function?

Step 2 – count how many birthdays are shared

get_shared_birthdays <- function(n = 50){
  
  bday_data <- tibble(person = 1:n,
                      bday   = sample(1:365, 
                                      size = n, 
                                      replace = TRUE)
                      )
  
  double_bdays <- bday_data |> 
    count(bday) |> 
    filter(n >= 2) |> 
    nrow()
  
}

Step 3 – return whether or not a shared birthday exists

get_shared_birthdays <- function(n = 50){
  bday_data <- tibble(person = 1:n,
                      bday   = sample(1:365, 
                                      size = n, 
                                      replace = T)
                      )
  
  double_bdays <- bday_data |> 
    count(bday) |> 
    filter(n >= 2) |> 
    nrow()
  
  double_bdays > 0
}

What type of output is this function returning?

Using Function to Simulate Many Probabilities

Use a map() function to simulate 1000 datasets.

set.seed(14)

sim_results <- map_lgl(.x = 1:1000,
                       .f = ~ get_shared_birthdays(n = 50))


  • What proportion of these datasets contain at least two people with the same birthday?
sum(sim_results) / length(sim_results)
[1] 0.96

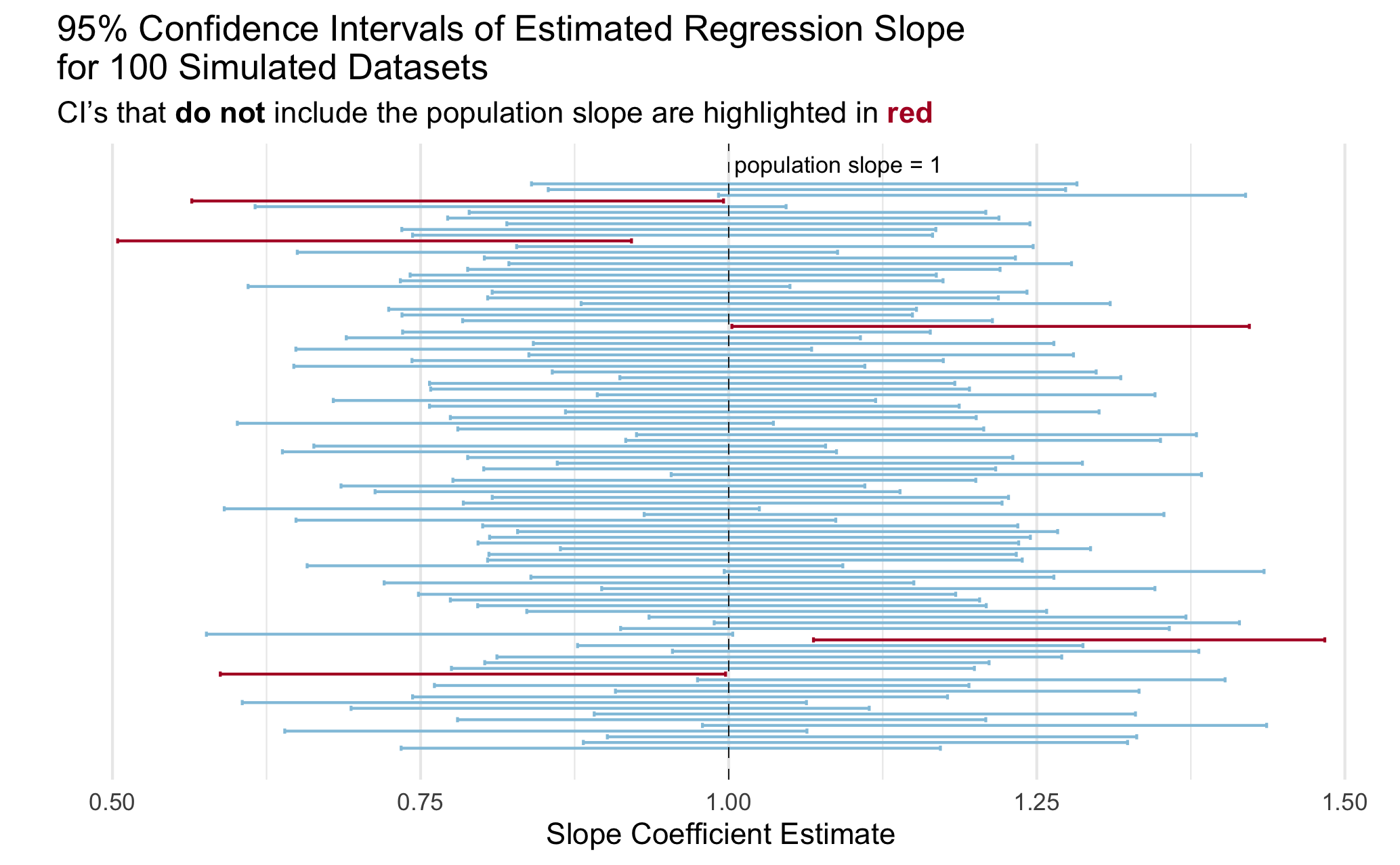
Lab 9: Simulating Confidence Interval Coverage Rates

Simple Linear Regression (SLR)

If we assume the relationship between \(x\) and \(y\) takes the form of a linear function…

\[ response = intercept + slope \times explanatory + noise \]

SLR Model Notation

In Statistics, there are two types of models—the population model and the fitted (sample) model.

Population Regression Model

\(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\)

where \(\epsilon_i \sim N(0, \sigma)\) is the random noise.

Fitted Regression Model

\(\widehat{y}_i = \widehat{\beta}_0 + \widehat{\beta}_1 x_i\)

where   \(\widehat{}\)   indicates the value was estimated.

Fitting an SLR Model

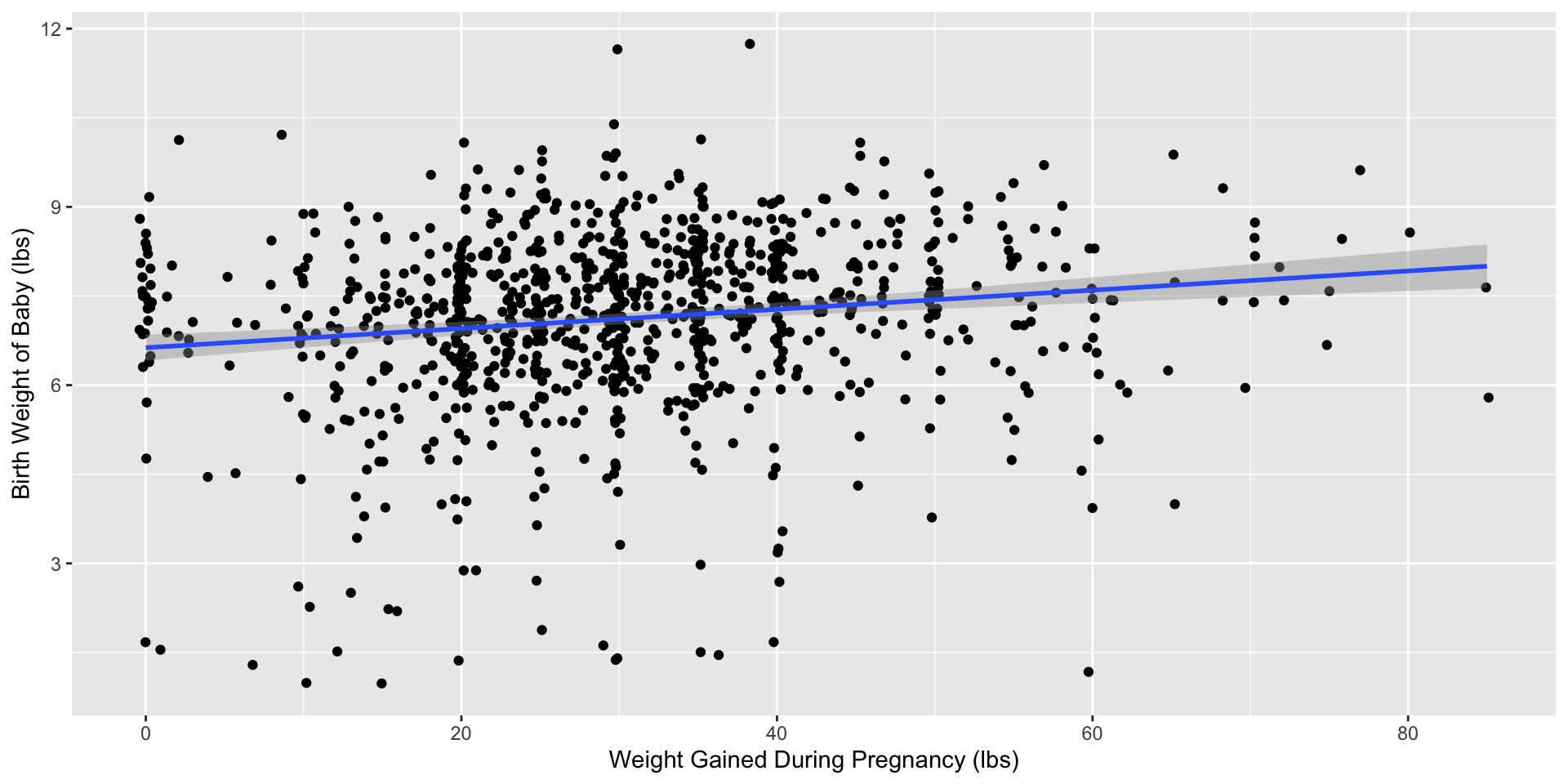
Regress baby birthweight (response variable) on the pregnant parent’s weight gain (explanatory variable).

  • We are assuming there is a linear relationship between how much weight the parent gains and how much the baby weighs at birth.

When visualizing data, fit a regression line (\(y\) on \(x\)) to your scatterplot.

ncbirths |> 
  ggplot(aes(x = gained, y = weight)) +
  geom_jitter() + 
  geom_smooth(method = "lm") +
  labs(x = "Weight Gained During Pregnancy (lbs)", 
       y = "Birth Weight of Baby (lbs)")

The lm() function fits a linear regression model.

  • We use formula notation to specify the response variable (LHS) and the explanatory variable (RHS).
  • This code creates an lm object.
ncbirth_lm <- lm(weight ~ gained, 
                 data = ncbirths)

Model Outputs

summary(ncbirth_lm)

Call:
lm(formula = weight ~ gained, data = ncbirths)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.4085 -0.6950  0.1643  0.9222  4.5158 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.63003    0.11120  59.620  < 2e-16 ***
gained       0.01614    0.00332   4.862 1.35e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.474 on 971 degrees of freedom
  (27 observations deleted due to missingness)
Multiple R-squared:  0.02377,   Adjusted R-squared:  0.02276 
F-statistic: 23.64 on 1 and 971 DF,  p-value: 1.353e-06
coefficients(ncbirth_lm)
(Intercept)      gained 
 6.63003358  0.01614049


To grab the slope estimate we would need to…

coefficients(ncbirth_lm)[2]
    gained 
0.01614049

…but we don’t have any measure of uncertainty!

broom::tidy(ncbirth_lm, 
            conf.int = TRUE, 
            conf.level = 0.9)
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 6.6300336 0.1112054 59.619718 0.0e+00 6.4469423 6.8131248
gained 0.0161405 0.0033195 4.862253 1.4e-06 0.0106751 0.0216059

Confidence Level

You can change the confidence level for the confidence interval in the conf.level argument!

Grabbing Model Outputs

broom::tidy(ncbirth_lm, 
            conf.int = TRUE, 
            conf.level = 0.9) |> 
  filter(term == "gained") |> 
  select(estimate, conf.low, conf.high)
# A tibble: 1 × 3
  estimate conf.low conf.high
     <dbl>    <dbl>     <dbl>
1   0.0161   0.0107    0.0216

Our Goal

A horizontal plot showing 100 simulated 95% confidence intervals (CIs) for estimated regression slopes. Each horizontal line represents one simulated dataset’s estimated slope and its 95% CI. Most intervals are drawn in light blue, while a few are in red—these red lines indicate CIs that do not include the true population slope. A vertical dashed line marks the population slope at 1. The title reads '95% Confidence Intervals of Estimated Regression Slope for 100 Simulated Datasets,' and a caption explains that intervals not including the population slope are highlighted in red. The distribution of intervals is roughly centered around the true slope of 1, with a few red intervals missing it on either side.

Lab 8 Revisions

Lab 8 Revisions

Only problems receiving a growing can be submitted for additional feedback!

I have left many of you comments on changes to make to your code that I trust you can do on your own!

Lab 8 Feedback

Q1: How can you make your code more clear? Argument names?

Q1: How can you make your code more robust? Using ~ to define a function? Using .x to indicate where the input should go?

Q1 & Q3: How can you incorporate input checks into your function? Checking if the input is a data frame? Checking if the variables are the right data type? Checking if the variables are included in the data frame?

Q5: Can you give your function a name that describes what it does? (e.g., make_filled_barplot(), make_colored_scatterplot())

Q5: We haven’t learned paste() or paste0() in this class! What functions have we learned that executed this process?

Survey on Experiences in STAT 331 / 531

Anonymous Google Form: https://forms.gle/YzZWe2oJZ5eWyTbRA

If we get an 85% completion rate I will bring doughnuts to class next Thursday!