Simulating Data in R

Today we will…

• Plan for Week 9 & 10
• Survey on Group Collaborations
• New Material
  • Statistical Distributions
  • Simulating Data
• PA 9: Instrument Con

Week 9

• PA 10 (today)
• Lab 10 (last one!)
• Revisions on Lab 8 (due Friday)

Week 10

• Revisions on Lab 9 (due Monday)
• Final Portfolio Week!

Warning

No revisions will be accepted on Lab 10. You can, however, talk with me during class about any questions you have. :)

Researching Survey Design

5-minutes

If you would like to participate

• Complete consent form (say yes)

If you would not like to participate

• Complete consent form (say no)

Statistical Distributions

Statistical Distributions

Recall from your statistics classes…

• Random Variable
• Distribution

A random variable is a value we don’t know until we take a sample.

• Coin flip: could be heads (0) or tails (1)
• Person’s height: could be anything from 0 feet to 10 feet.
• Annual income of a US worker: could be anything from $0 to $1.6 billion

The distribution of a random variable tells us its possible values and how likely they are to occur.

• Coin flip: 50% chance of heads and tails.
• Heights follow a bell curve centered at 5 foot 7.
• Most American workers make under $100,000.

Statistical Distributions with Names!

• unif
• norm
• t
• chisq
• binom

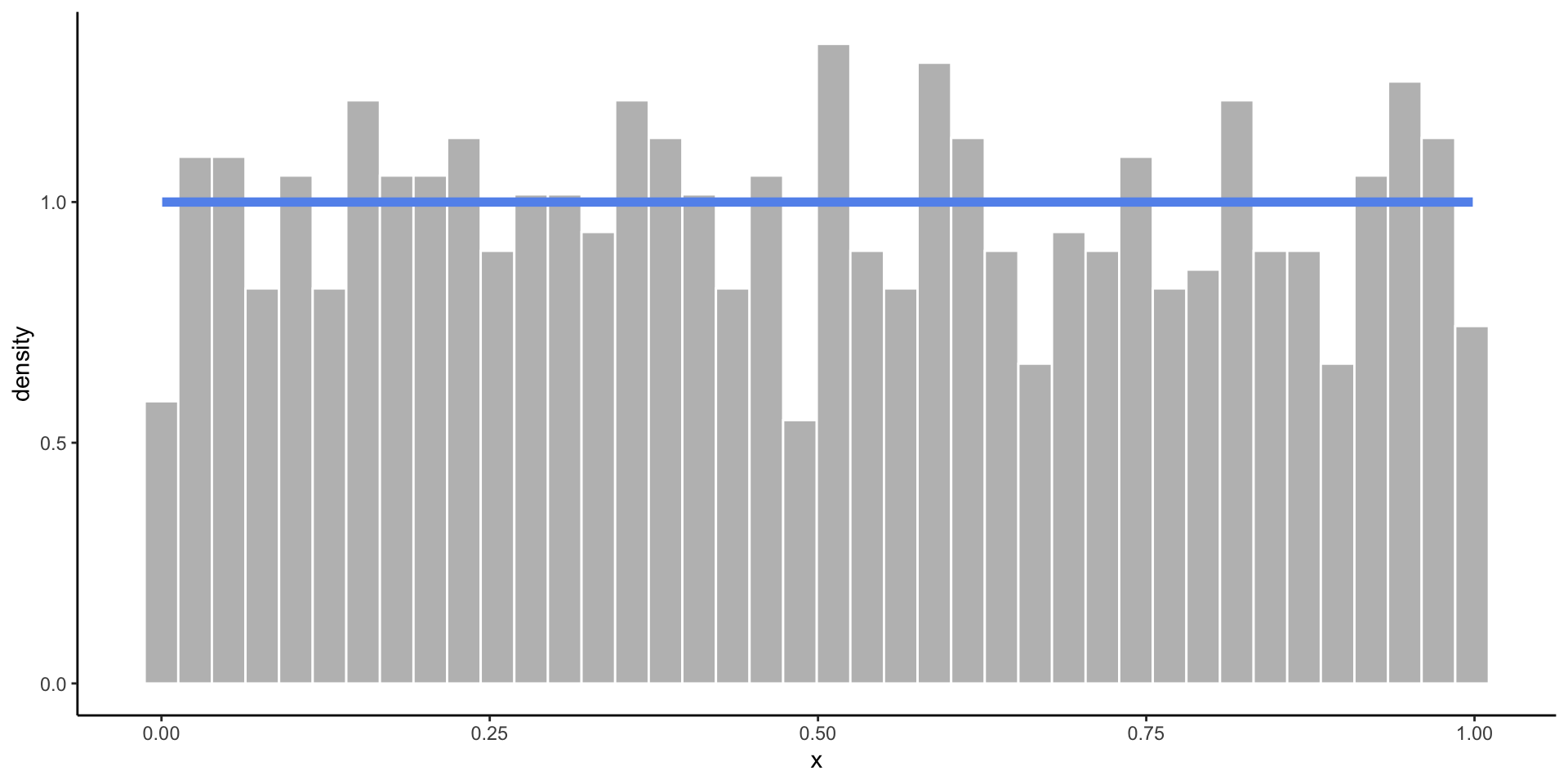
Uniform Distribution

• When you know the range of values, but not much else.
• All values in the range are equally likely to occur.

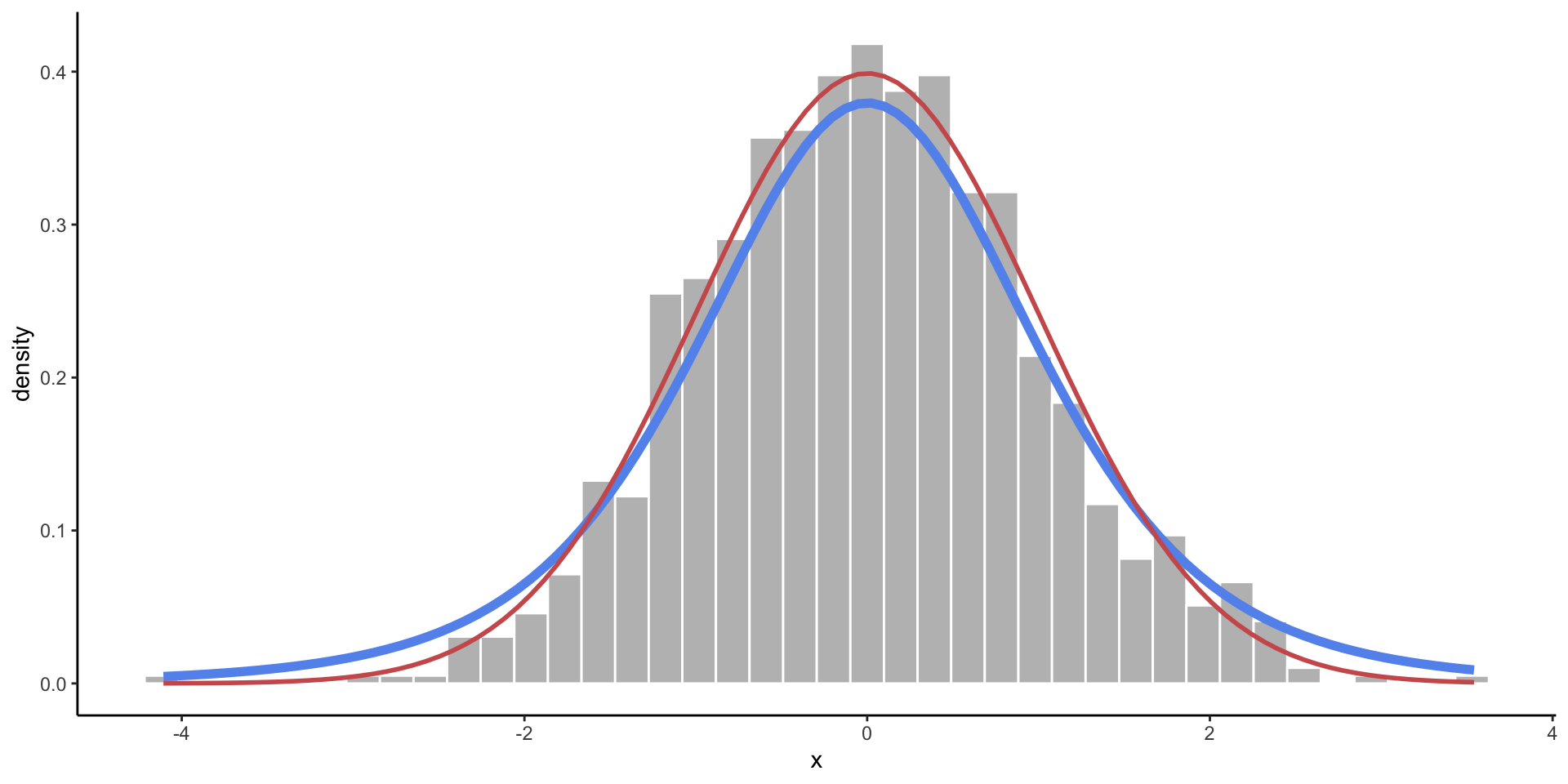
Normal Distribution

• When you expect most values to fall near the center.
• Frequency of values follows a bell shaped curve.

t-Distribution

• A slightly wider bell curve.
• Basically used in the same context as the Normal distribution, but more common with real data (when the standard deviation is unknown).

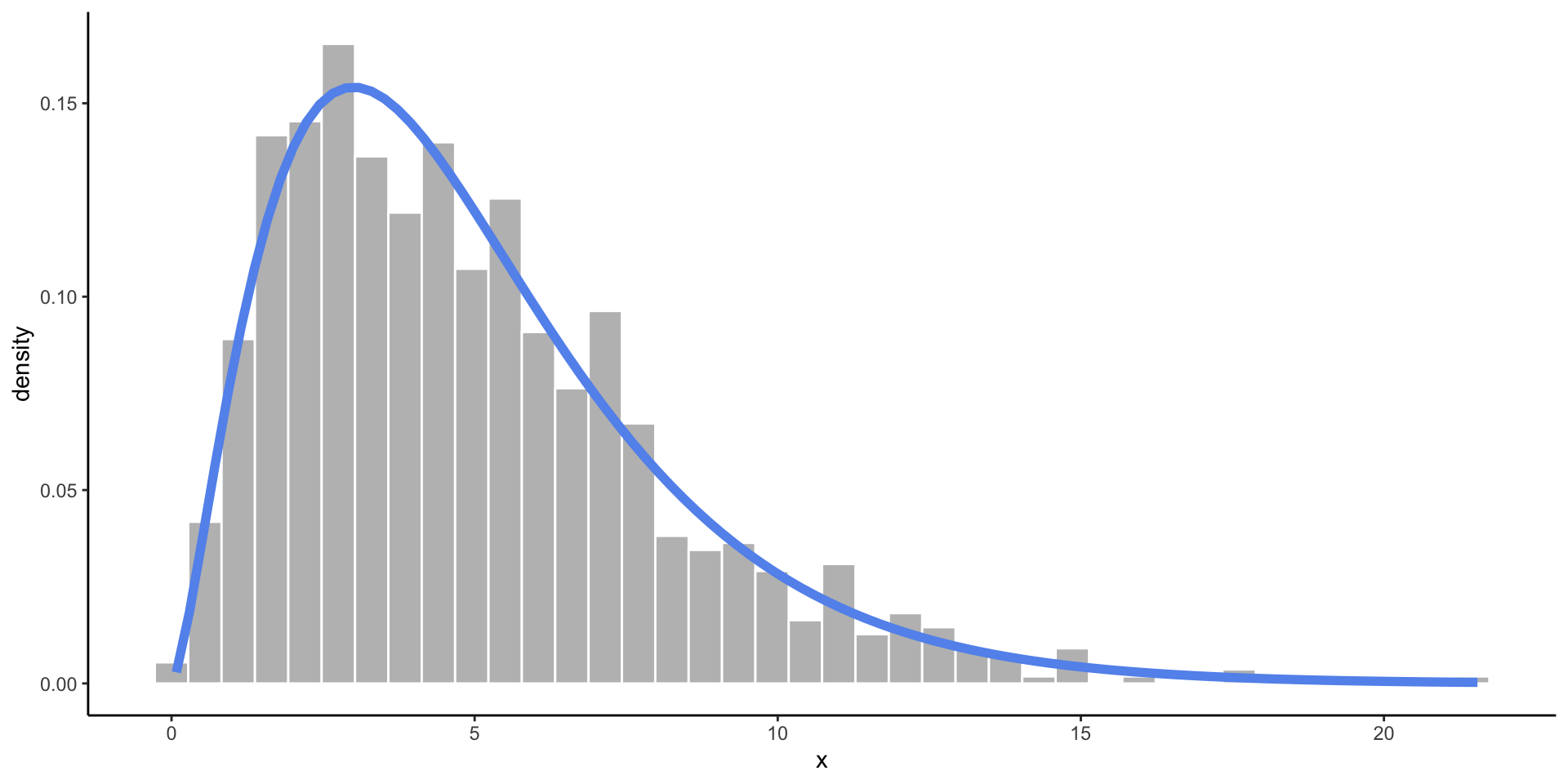
Chi-Square Distribution

• Somewhat skewed, and only allows values above zero.
• Used in testing count data.

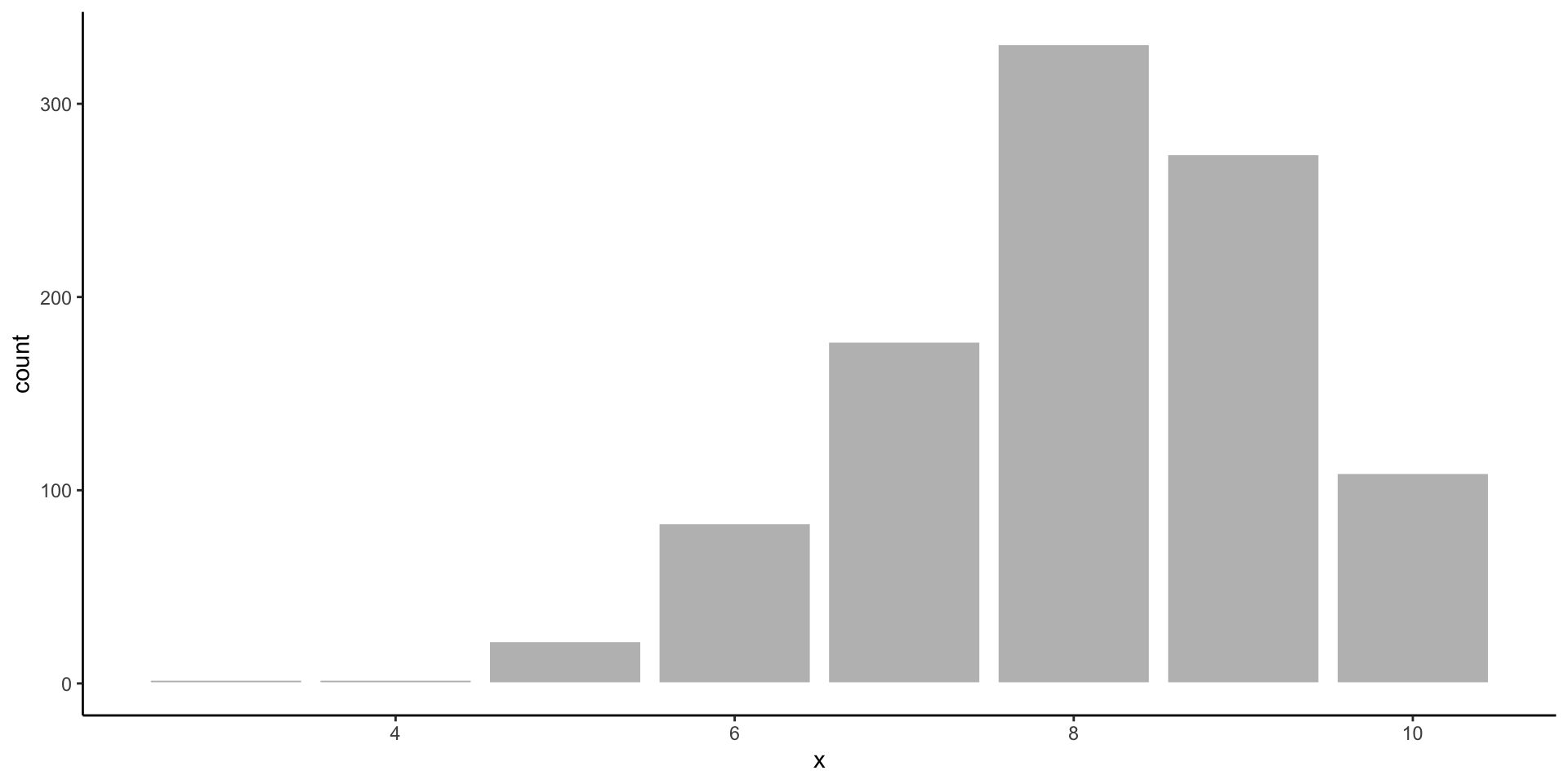
Binomial Distribution

• Appears when you have two possible outcomes, and you are counting how many times each outcome occurred.
• This is a discrete distribution, as there can only be whole number values!

Distribution Functions in R

• r
• p
• q
• d

r is for random sampling.

• Generate random values from a distribution.
• We use this to simulate data (create pretend observations).

runif(n = 3, 
      min = 10, 
      max = 20)

[1] 15.25854 10.39408 13.67694

rnorm(n = 3, 
      mean = 5, 
      sd = 2)

[1] 4.709666 3.216237 3.689576

rt(n = 3, 
   df = 11)

[1]  0.7794292 -1.3851774  0.3020068

rbinom(n = 3, 
       size = 10, 
       prob = 0.7)

[1] 8 9 7

p is for probability.

• Compute the chances of observing a value less than (or greater than) x.

pchisq(q = 2, 
      df = 8)

[1] 0.01898816

pchisq(q = 2, 
      df = 8, 
      lower.tail = FALSE)

[1] 0.9810118

1 - pchisq(q = 2, 
      df = 8)

[1] 0.9810118

q is for quantile.

• Given a probability \(p\), compute \(x\) such that \(P(X < x) = p\).
• The q functions are “backwards” of the p functions.

qt(p = 0.95,
   df = 12)

[1] 1.782288

qt(p = 0.95,
   df = 30)

[1] 1.697261

d is for density.

• Compute the height of a distribution curve at a given \(x\).
• For discrete dist: probability of getting exactly \(x\).
• For continuous dist: usually meaningless.

Probability of exactly 12 heads in 20 coin tosses, with a 50% chance of tails?

dbinom(x = 12, size = 20, prob = 0.5)

[1] 0.1201344

Simulating Data

Simulate a Dataset

• The Idea
• set.seed()
• tibble()
• visualize

We can generate fake data based on the assumption that a variable follows a certain distribution.

• We randomly sample observations from the distribution.

age <- runif(n = 1000, 
             min = 15, 
             max = 75)

Since there is randomness involved, we will get a different result each time we run the code.

runif(n = 3, min = 15, max = 75)

[1] 67.48274 41.72524 71.36765

runif(n = 3, min = 15, max = 75)

[1] 31.79127 32.91463 26.24914

To make a reproducible random sample, we first set the seed:

set.seed(93401)
runif(n = 3, min = 15, max = 75)

[1] 20.84739 51.61768 42.68515

set.seed(93401)
runif(n = 3, min = 15, max = 75)

[1] 20.84739 51.61768 42.68515

set.seed(435)

fake_data <- tibble(names   = charlatan::ch_name(n = 1000),
                    age     = runif(n = 1000, min = 18, max = 29),
                    mamdani = rbinom(n = 1000, size = 1, prob = 0.75)
                    ) |> 
  mutate(supports_mamdani = ifelse(mamdani == 1, "yes", "no"))

head(fake_data)

# A tibble: 6 × 4
  names                   age mamdani supports_mamdani
  <chr>                 <dbl>   <int> <chr>           
1 Elbridge Kautzer       24.1       0 no              
2 Brandon King           26.0       1 yes             
3 Phyllis Thompson       20.8       1 yes             
4 Humberto Corwin        28.9       0 no              
5 Theresia Koelpin       25.1       0 no              
6 Hayden O'Reilly-Johns  28.6       1 yes             

Check to see the ages look uniformly distributed.

fake_data |> 
  ggplot(mapping = aes(x = age,
                       fill = supports_mamdani)) +
  geom_histogram(show.legend = F) +
  facet_wrap(~ supports_mamdani,
             ncol = 1) +
  scale_fill_brewer(palette = "Paired") +
  theme_bw() +
  labs(x = "Age (years)",
       y = "",
       subtitle = "Number of Individuals Supportng Prop 50 for Different Ages",)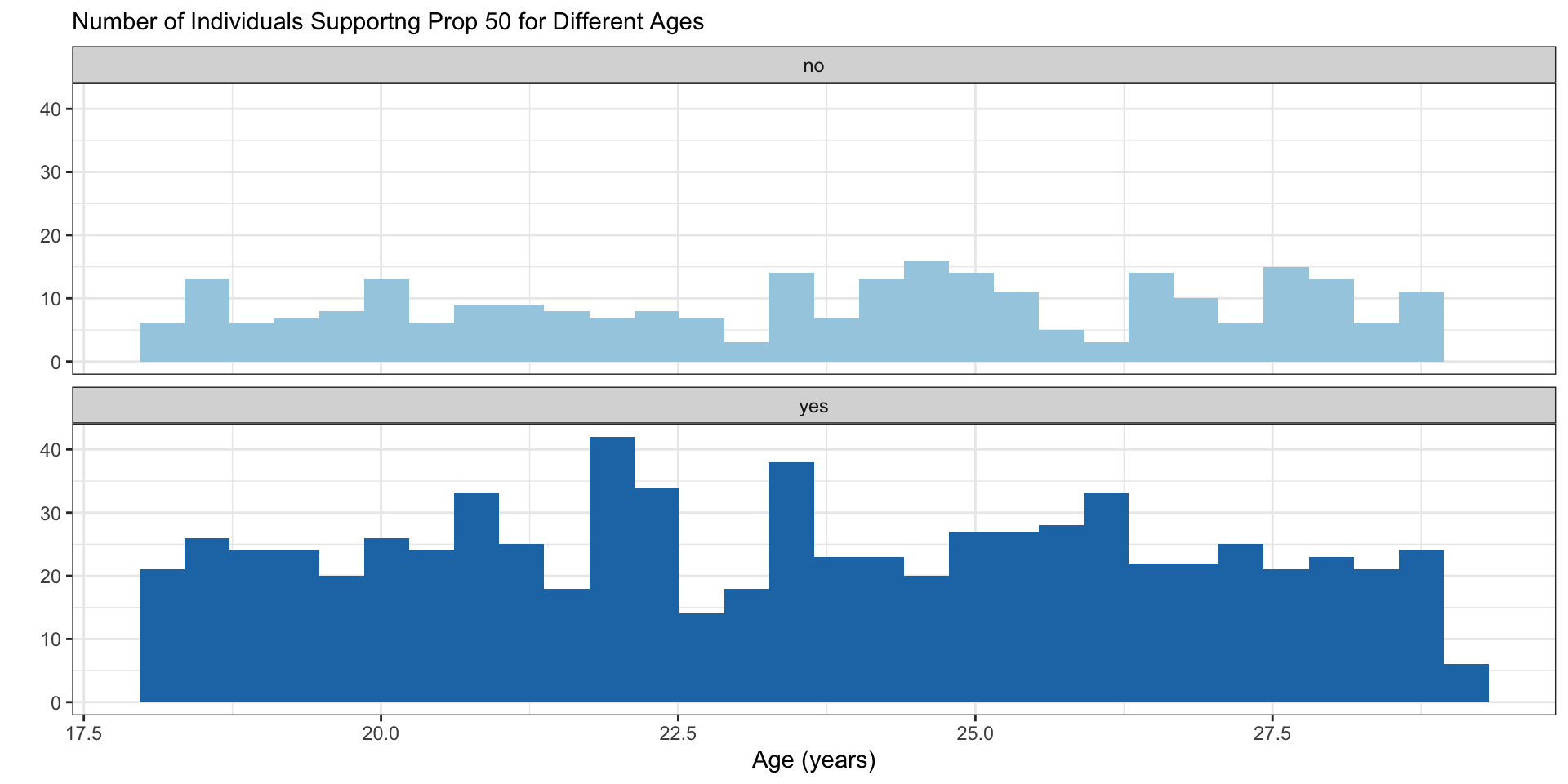

PA 9: Instrument Con

Is the instrument salesman selling fake instruments?

PA 9

In this practice activity you and your partner will write a function to simulate the weight of various band instruments, with the goal of identifying whether a particular shipment of instruments has a “reasonable” weight.

This activity will require knowledge of:

• named distributions
• probability calculations related to distributions
• function documentation
• function syntax
• function arguments

None of us have all these abilities. Each of us has some of these abilities.

A reminder about boolean values…

Suppose x is Normally distributed with mean 5 and standard deviation 2.

We would expect about 15.87% percent of values to be below 3. Let’s see if that is the case!

Simulate 1000 values of x.

sims <- rnorm(n = 1000, mean = 5, sd = 2)

A reminder about boolean values…

How many values were below 3?

sims < 3

   [1] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
  [13]  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
  [25] FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE
  [37] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE
  [49] FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
  [61] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE
  [73] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
  [85] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
  [97] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
 [109] FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [121] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [133]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
 [145] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE
 [157] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE
 [169] FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE
 [181] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE
 [193] FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
 [205]  TRUE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [217] FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE
 [229] FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE FALSE  TRUE FALSE FALSE FALSE
 [241]  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
 [253] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [265] FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
 [277] FALSE  TRUE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [289] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [301]  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE  TRUE
 [313] FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE  TRUE FALSE FALSE
 [325] FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
 [337] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE
 [349] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [361] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [373] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [385] FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE
 [397] FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
 [409] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE
 [421] FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
 [433]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE
 [445] FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [457] FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE
 [469] FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE
 [481] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
 [493]  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE
 [505] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
 [517] FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [529] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE
 [541] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [553]  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [565]  TRUE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
 [577] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE FALSE
 [589]  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [601] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
 [613] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
 [625] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE
 [637] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
 [649] FALSE  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE
 [661]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
 [673] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [685]  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE  TRUE
 [697]  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [709] FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE
 [721] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
 [733] FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
 [745] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [757]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
 [769] FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [781] FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE  TRUE  TRUE FALSE FALSE
 [793] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [805] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [817] FALSE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE
 [829] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [841] FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
 [853] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [865] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [877] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [889] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
 [901]  TRUE FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE FALSE
 [913] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [925]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [937] FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
 [949] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
 [961] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
 [973] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
 [985] FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE
 [997] FALSE  TRUE FALSE FALSE

sum(sims < 3)

[1] 167

sum(sims < 3) / length(sims)

[1] 0.167

( sum(sims < 3) / 
    length(sims) ) * 100

[1] 16.7

Submission

You and your partner together should address the following questions:

How many simulated shipments had a weight less than or equal to Professor Hill’s shipment?

Do you beleive Professor Hill ordered genuine instruments?

5-minute break

Team Assignments - 9am

The partner whose birthday is the closest to today starts as the Talker!

Team Assignments - 12pm

The partner whose birthday is the closest to today starts as the Talker!