Distances Between Observations

More words about ChatGPT…

What is my job?


Teaching you stuff


(Thoughtfully) choosing what to teach and how to teach it.

Assessing what you’ve learned


What do you understand about the tools I’ve taught you?


This is not the same as assessing if you figured out a way to accomplish a given task.

Using the tools I teach

is_100m = df_bolt["Event"] == "2008 Olympics 100m"
df_100m = df_bolt[is_100m]
one_mean = df_100m["Time"].mean()
one_std = df_100m["Time"].std()

df_bolt["Standardized_Time"] = 0.0
df_bolt.loc[is_100m, "Standardized_Time"] = (df_bolt.loc[is_100m, "Time"] - 


event_stats = df_phelps.groupby('Event')['Time_in_seconds'].agg(['mean', 'std'])
df_phelps = df_phelps.merge(event_stats, on='Event')
df_phelps['Standardized_Time'] = (
(df_phelps['Time_in_seconds'] - df_phelps['mean']) / df_phelps['std']
)

A nice clean, efficient approach

bolt_stats = (
  df_bolt
  .groupby("Event")["Time"]
  .aggregate(["mean", "std"])
  )

standardized_bolt = (
  df_bolt
  .set_index(['Event', 'Athlete'])['Time']
  .subtract(bolt_stats["mean"])
  .divide(bolt_stats["std"])
  )

lambda Functions

phelps_sec = (
  df_phelps["Time"]
  .str.split(":")
  .apply(lambda x: float(x[0])*60 + float(x[1]))
)


df_phelps[["Minutes", "Seconds"]] = df_phelps["Time"].str.split(":")
df_phelps["Time_New"] = (
  df_phelps["Minutes"].astype(float) * 60 +
  df_phelps["Seconds"].astype(float)
  )

A loop is often not necessary

split_times = df_phelps["Time"].str.split(":")
seconds = []

for time in split_times:
  minute = int(time[0])
  second = float(time[1])
  seconds.append((minute * 60) + second)
  df_phelps["Seconds"] = seconds

When to make a function?

def time_to_secs(time_str):
  mins, secs = time_str.split(':')
  return float(mins) * 60 + float(secs)

df_phelps['time_secs'] = df_phelps['Time'].apply(time_to_secs)


def calculate_simpson_index(values, position):
    
    # Convert values to a Pandas Series, ensuring they are strings
    values_series = pd.Series(values).astype(str)
    
    # Extract the specified character based on the position
    extracted_character = values_series.str[position]
    
    # Calculate the frequency of each character
    character_counts = extracted_character.value_counts(normalize=True)
    
    # Compute the Simpson's Index
    simpson_index = 1 - sum(character_counts ** 2)
    
    return simpson_index

The story so far…

Summarizing

  • One categorical variable: marginal distribution

  • Two categorical variables: joint and conditional distributions

  • One quantitative variable: mean, median, variance, standard deviation.

  • One quantitative, one categorical: mean, median, and std dev across groups (groupby(), split-apply-combine)

  • Two quantitative variables: z-scores, correlation

Visualizing

  • One categorical variable: bar plot or column plot

  • Two categorical variables: stacked bar plot, side-by-side bar plot, or stacked percentage bar plot

  • One quantitative variable: histogram, density plot, or boxplot

  • One quantitative, one categorical: overlapping densities, side-by-side boxplots, or facetting

  • Two quantitative variables: scatterplot

Today’s data: House prices

Ames house prices

df = pd.read_table("https://datasci112.stanford.edu/data/housing.tsv",
                    sep = "\\t")
df.head()
         PID  Gr Liv Area  Bedroom AbvGr  ...  Sale Type  Sale Condition  SalePrice
0  526301100         1656              3  ...        WD           Normal     215000
1  526350040          896              2  ...        WD           Normal     105000
2  526351010         1329              3  ...        WD           Normal     172000
3  526353030         2110              3  ...        WD           Normal     244000
4  527105010         1629              3  ...        WD           Normal     189900

[5 rows x 81 columns]

read_table not read_csv

This is a tsv file (tab separated values), so we need to use a different function to read in our data! The sep argument allows you to specify the delimiter the file uses, but you can also allow the system to autodetect the delimiter.

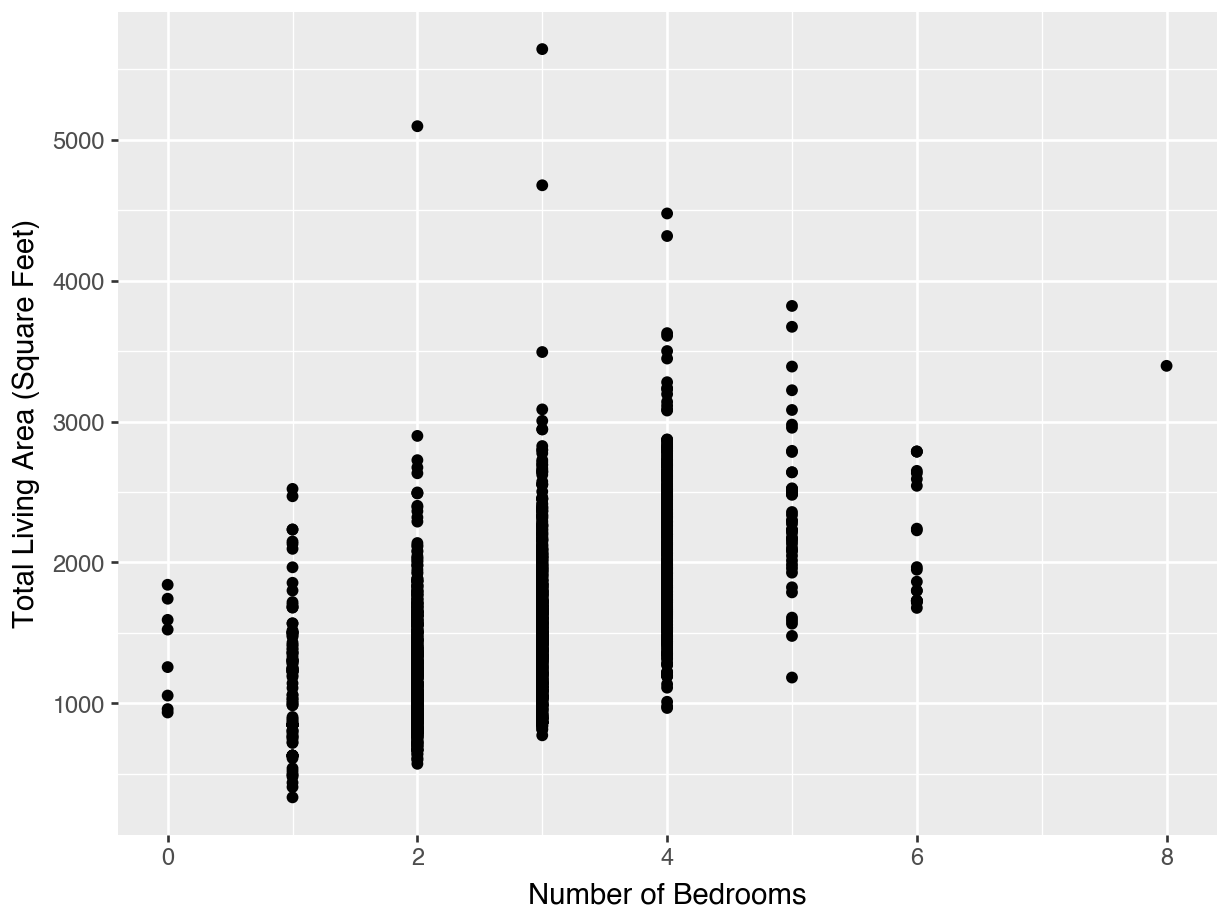
How does house size relate to number of bedrooms?

Code 
(
  ggplot(df, mapping = aes(x = "Gr Liv Area", y = "Bedroom AbvGr"))  + 
  geom_point() +
  labs(x = "Total Living Area", 
       y = "Number of Bedrooms")
 )

How does house size relate to number of bedrooms?

What statistic would you calculate?

df[["Gr Liv Area", "Bedroom AbvGr"]].corr()
               Gr Liv Area  Bedroom AbvGr
Gr Liv Area       1.000000       0.516808
Bedroom AbvGr     0.516808       1.000000

Measuring Similarity with Distance

Similarity

How might we answer the question, “Are these two houses similar?”

df.loc[1707, ["Gr Liv Area", "Bedroom AbvGr"]]
Gr Liv Area      2956
Bedroom AbvGr       5
Name: 1707, dtype: object
df.loc[290, ["Gr Liv Area", "Bedroom AbvGr"]]
Gr Liv Area      2650
Bedroom AbvGr       6
Name: 290, dtype: object

Distance

The distance between the two observations is:

\[ \sqrt{ (2956 - 2650)^2 + (5 - 6)^2} = 306 \]

… what does this number mean? Not much!

But we can use it to compare sets of houses and find houses that appear to be the most similar.

Another House to Consider

df.loc[1707, ["Gr Liv Area", "Bedroom AbvGr"]]
Gr Liv Area      2956
Bedroom AbvGr       5
Name: 1707, dtype: object
df.loc[291, ["Gr Liv Area", "Bedroom AbvGr"]]
Gr Liv Area      1666
Bedroom AbvGr       3
Name: 291, dtype: object

\[ \sqrt{ (2956 - 1666)^2 + (5 - 3)^2} = 1290 \]

Thus, house 1707 is more similar to house 290 than to house 291.

Lecture Activity Part 1

Complete Part One of the activity linked in Canvas.

10:00

Scaling / Standardizing

House 160 seems more similar…

Code 
(
  ggplot(df, mapping = aes(y = "Gr Liv Area", x = "Bedroom AbvGr")) + 
  geom_point(color = "lightgrey") + 
  geom_point(df.loc[[1707]], color = "red", size = 2, shape = 17) + 
  geom_point(df.loc[[160]], color = "blue", size = 2) + 
  geom_point(df.loc[[2336]], color = "green", size = 2) + 
  theme_bw() +
  labs(y = "Total Living Area (Square Feet)", 
       x = "Number of Bedrooms")
)

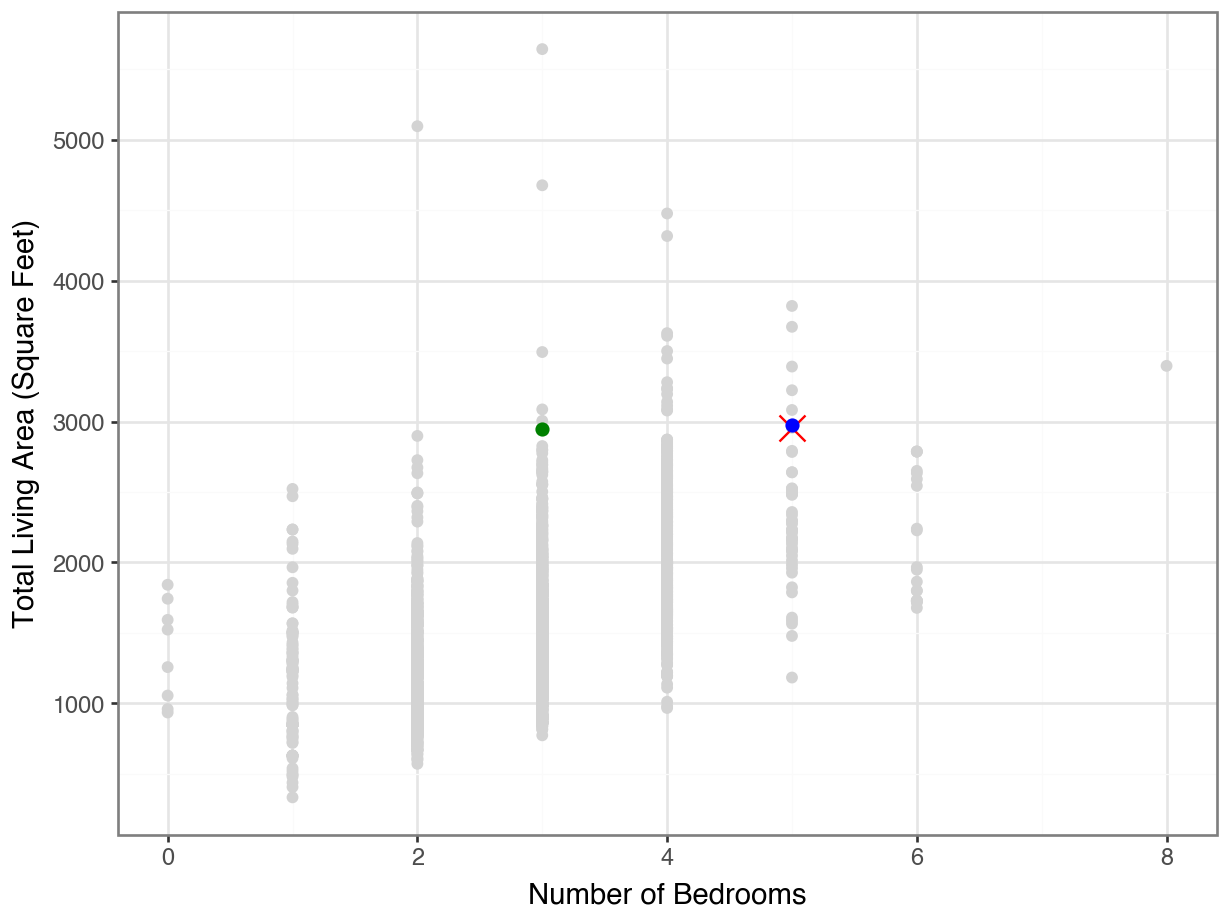
…even if we zoom in…

Code 
(
  ggplot(df, mapping = aes(y = "Gr Liv Area", x = "Bedroom AbvGr")) + 
  geom_point(color = "lightgrey") + 
  geom_point(df.loc[[1707]], color = "red", size = 5, shape = "x") + 
  geom_point(df.loc[[160]], color = "blue", size = 2) + 
  geom_point(df.loc[[2336]], color = "green", size = 2) + 
  theme_bw() +
  labs(y = "Total Living Area (Square Feet)", 
       x = "Number of Bedrooms") +
  scale_y_continuous(limits = (2500, 3500))
)

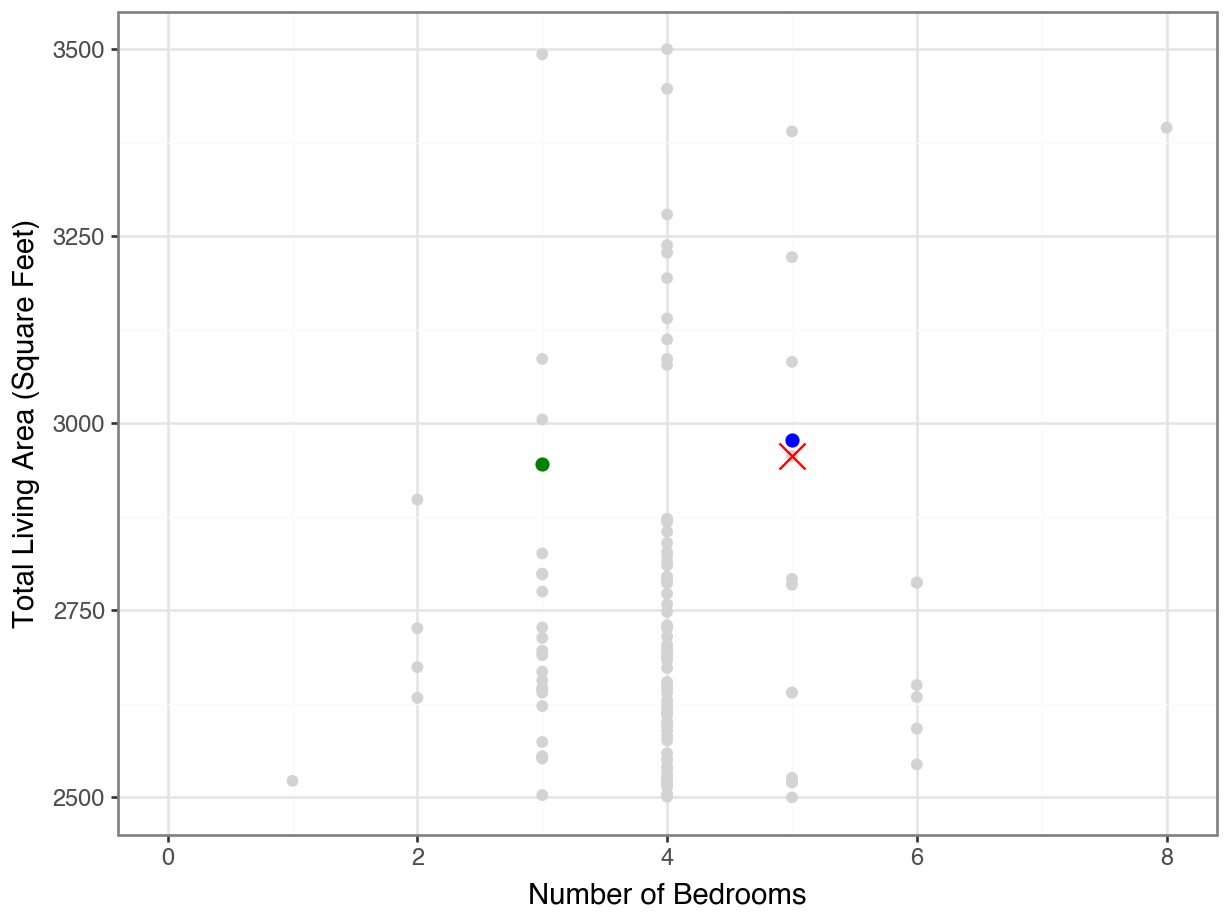
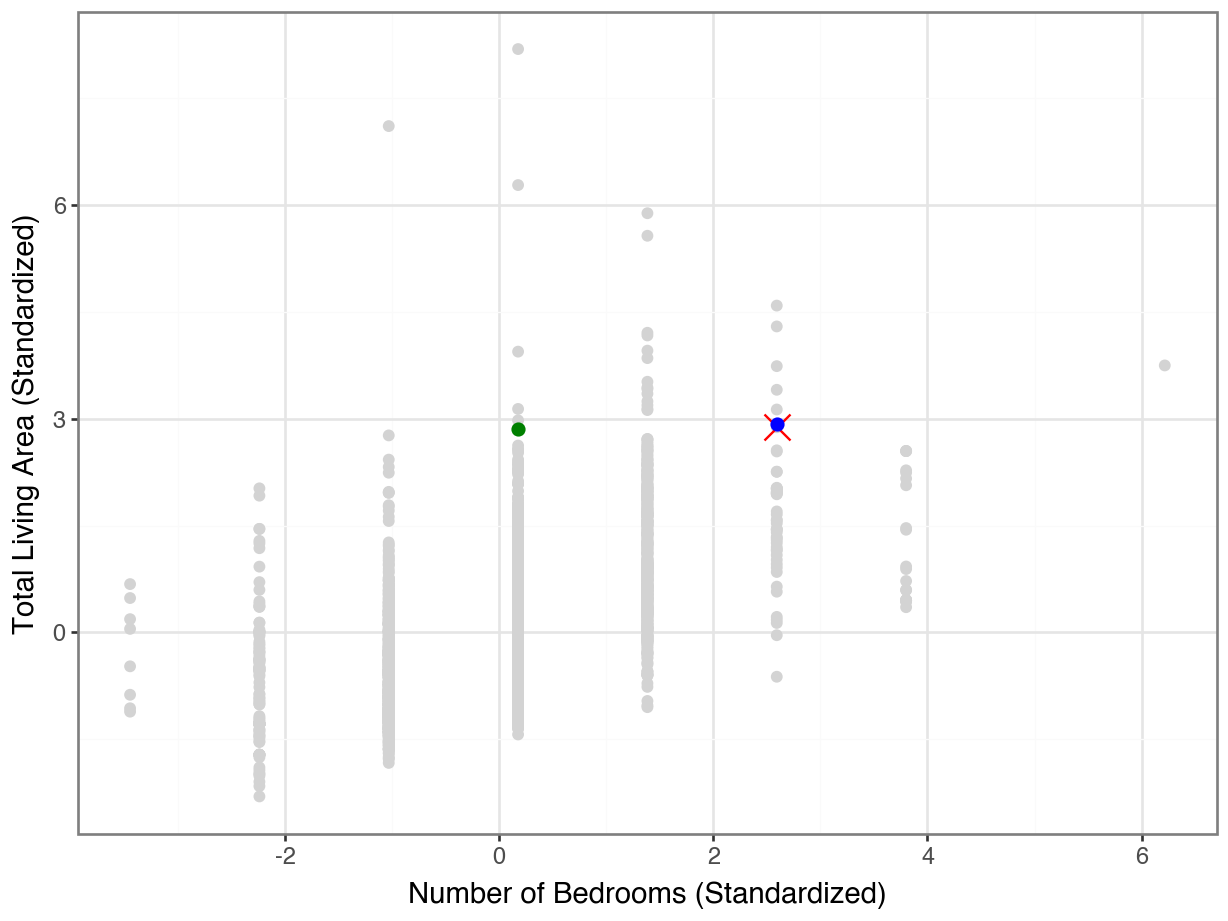
…but not if we put the axes on the same scale!

Code 
(
  ggplot(df, aes(y = "Gr Liv Area", x = "Bedroom AbvGr")) + 
  geom_point(color = "lightgrey") + 
  geom_point(df.loc[[1707]], color = "red", size = 5, shape = "x") + 
  geom_point(df.loc[[160]], color = "blue", size = 2) + 
  geom_point(df.loc[[2336]], color = "green", size = 2) + 
  theme_bw() +
  labs(y = "Total Living Area (Square Feet)", 
       x = "Number of Bedrooms") +
  scale_y_continuous(limits = (2900, 3000)) +
  scale_x_continuous(limits = (0, 100))
)

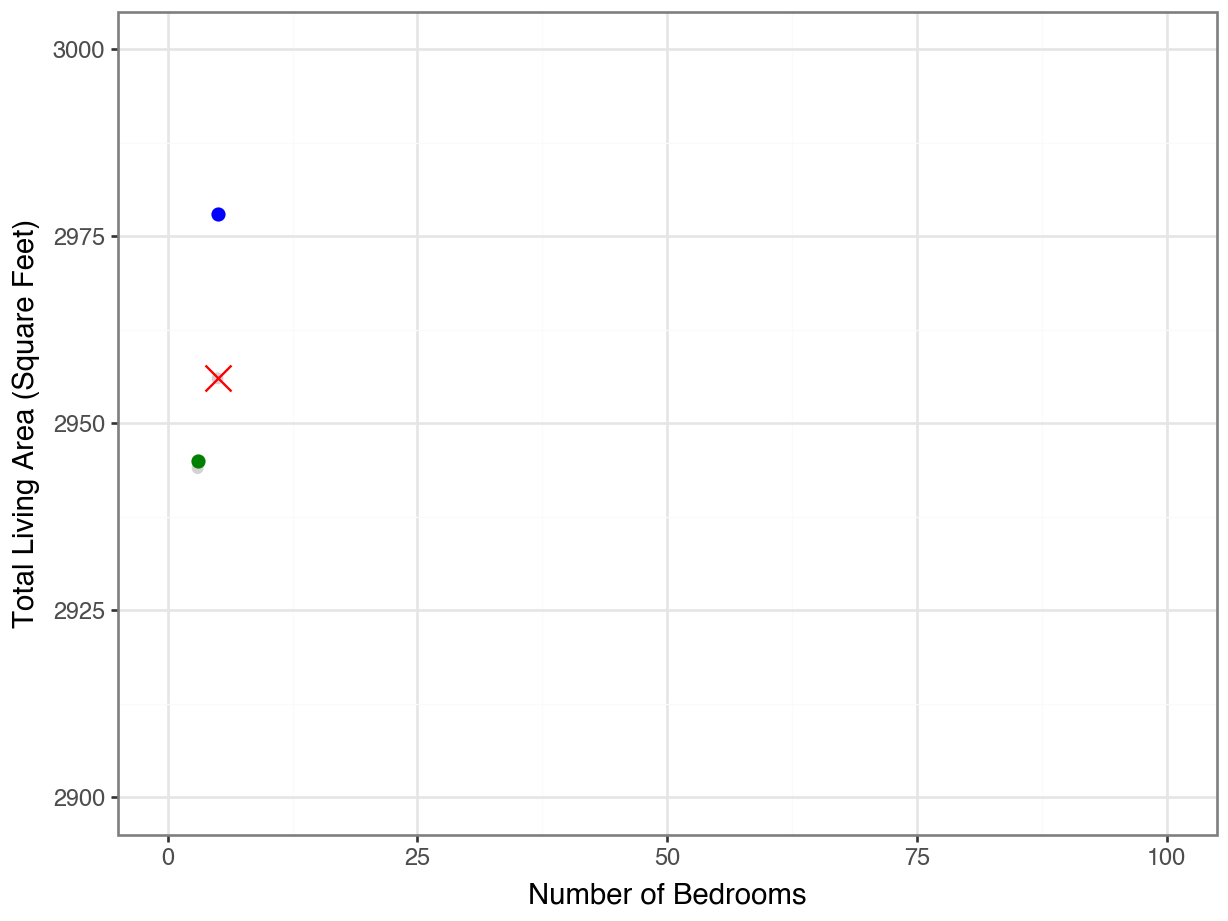
Scaling

We need to make sure our features are on the same scale before we can use distances to measure similarity.

Standardizing

subtract the mean, divide by the standard deviation

Scaling

df['size_scaled'] = (df['Gr Liv Area'] - df['Gr Liv Area'].mean()) / df['Gr Liv Area'].std()
df['bdrm_scaled'] = (df['Bedroom AbvGr'] - df['Bedroom AbvGr'].mean()) / df['Bedroom AbvGr'].std()
Code 
(
  ggplot(df, aes(y = "size_scaled", x = "bdrm_scaled")) + 
  geom_point(color = "lightgrey") + 
  geom_point(df.loc[[1707]], color = "red", size = 5, shape = "x") + 
  geom_point(df.loc[[160]], color = "blue", size = 2) + 
  geom_point(df.loc[[2336]], color = "green", size = 2) + 
  theme_bw() +
  labs(y = "Total Living Area (Standardized)", 
       x = "Number of Bedrooms (Standardized)") 
)

Lecture Activity Part 2

Complete Part Two of the activity linked in Canvas.

10:00

Scikit-learn

Scikit-learn

  • scikit-learn is a library for machine learning and modeling

  • We will use it a lot in this class!

  • For now, we will use it as a shortcut for scaling and for computing distances

  • The philosophy of sklearn is:

    • specify your analysis
    • fit on the data to prepare the analysis
    • transform the data

Specify

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
scaler
StandardScaler()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

No calculations have happened yet!

Fit

The scaler object “learns” the means and standard deviations.

df_orig = df[['Gr Liv Area', 'Bedroom AbvGr']]
scaler.fit(df_orig)
StandardScaler()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
scaler.mean_
array([1499.69044369,    2.85426621])
scaler.scale_
array([505.4226158 ,   0.82758988])

We still have not altered the data at all!

Transform

df_scaled = scaler.transform(df_orig)
df_scaled
array([[ 0.30926506,  0.17609421],
       [-1.19442705, -1.03223376],
       [-0.33771825,  0.17609421],
       ...,
       [-1.04801492,  0.17609421],
       [-0.21900572, -1.03223376],
       [ 0.9898836 ,  0.17609421]], shape=(2930, 2))

sklearn, numpy, and pandas

  • By default, sklearn functions return numpy objects.

  • This is sometimes annoying, maybe we want to plot things after scaling.

  • Solution: remake it, with the original column names.

pd.DataFrame(df_scaled, columns = df_orig.columns)
      Gr Liv Area  Bedroom AbvGr
0        0.309265       0.176094
1       -1.194427      -1.032234
2       -0.337718       0.176094
3        1.207523       0.176094
4        0.255844       0.176094
...           ...            ...
2925    -0.982723       0.176094
2926    -1.182556      -1.032234
2927    -1.048015       0.176094
2928    -0.219006      -1.032234
2929     0.989884       0.176094

[2930 rows x 2 columns]

Distances with sklearn

from sklearn.metrics import pairwise_distances

pairwise_distances(df_scaled[[1707]], df_scaled)
array([[3.52929876, 5.45459713, 4.0252646 , ..., 4.61305666, 4.76999349,
        3.06886734]], shape=(1, 2930))

Finding the Most Similar

dists = pairwise_distances(df_scaled[[1707]], 
                           df_scaled)
dists.argsort()
array([[1707,  160,  909, ...,  158, 2723, 2279]], shape=(1, 2930))
best = (
  dists
  .argsort()
  .flatten()
  [1:10]
  )
  
df_orig.iloc[best]
      Gr Liv Area  Bedroom AbvGr
160          2978              5
909          3082              5
1288         2792              5
2350         2784              5
253          3222              5
585          2640              5
2592         2640              5
2027         2526              5
2330         3390              5

Lecture Activity Part 3

Complete Part Three of the activity linked in Canvas.

10:00

Alternatives

Other scaling

  • Standardization \[x_i \leftarrow \frac{x_i - \bar{X}}{\text{sd}(X)}\]

  • Min-Max Scaling \[x_i \leftarrow \frac{x_i - \text{min}(X)}{\text{max}(X) - \text{min}(X)}\]

Other distances

  • Euclidean (\(\ell_2\))

    \[\sqrt{\sum_{j=1}^m (x_j - x'_j)^2}\]

  • Manhattan (\(\ell_1\))

    \[\sum_{j=1}^m |x_j - x'_j|\]

Lecture Activity Part 4

Complete Part Four of the activity linked in Canvas.

10:00

Takeaways

Takeaways

  • We measure similarity between observations by calculating distances.

  • It is important that all our features be on the same scale for distances to be meaningful.

  • We can use scikit-learn functions to fit and transform data, and to compute pairwise distances.

  • There are many options of ways to scale data; most common is standardizing

  • There are many options of ways to measure distances; most common is Euclidean distance.