Multivariate Summaries

Lab 1A Debrief

The Importance of Axis Labels

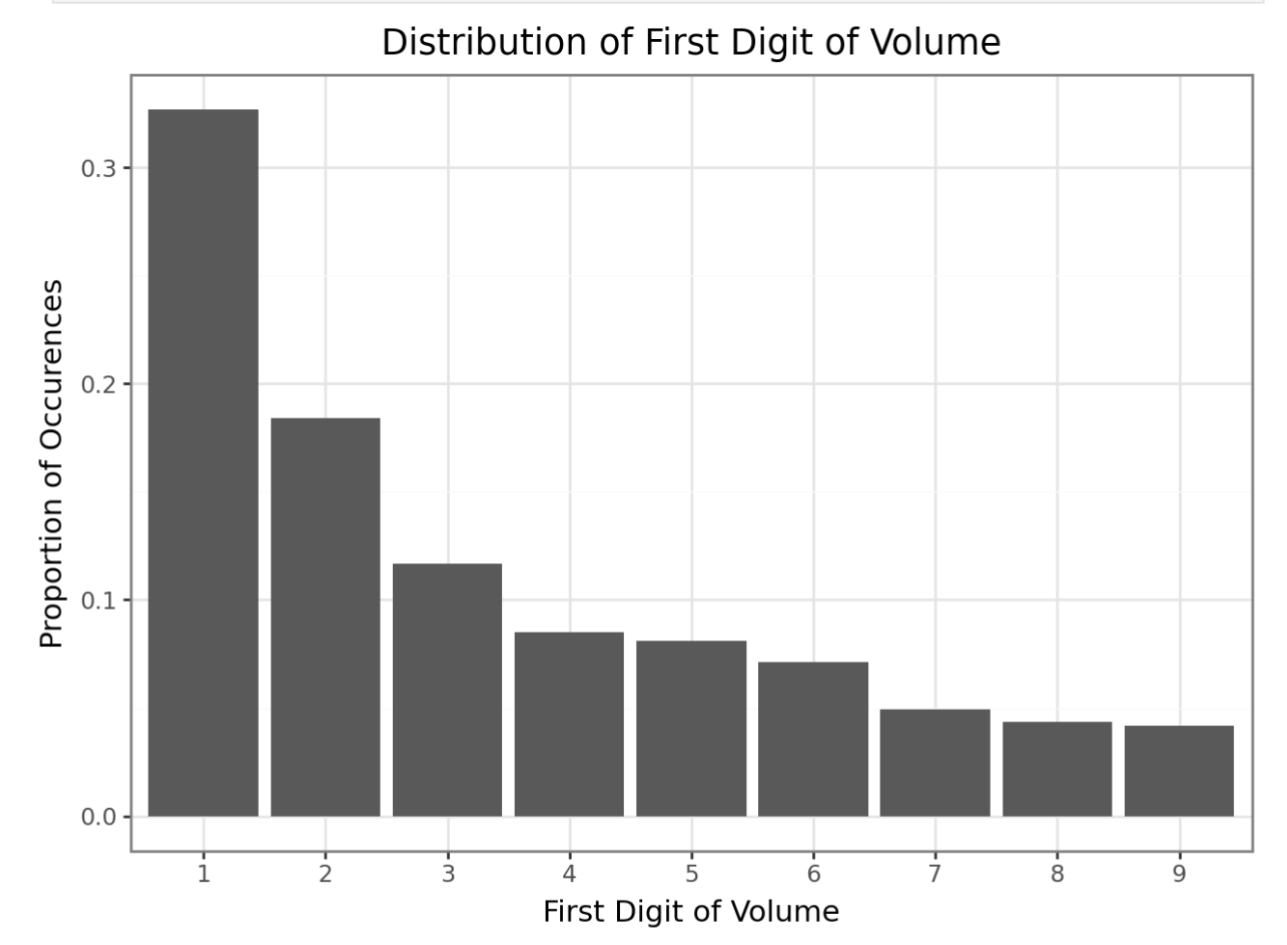
A plot of the proportion of the times the first digit of the volume of stocks sold by a stock market company started with each digit (1-9). The plot has an x-axis label describing the context of the digits ('First Digit of Volume') and the y-axis label describes the context of the proportions ('Proportion of Occurrances'). The plot title states 'Distribution of First Digit of Volume'.

Does your plot communicate the context of the data you are plotting?

The story so far…

Last Week

Reading in data and cleaning / prepping it.
Summarizing one categorical variable with a distribution.
Summarizing two categorical variables with joint and conditional distributions.
Using plotnine and the grammar of graphics to make bar plots and column plots.

Quantitative Variables So Far

Visualizing by converting to categorical.
Visualizing with histograms or densities.
Estimating probabilities from histograms and densities.
Describing the skew.
Calculating and explaining the mean and the median.
Calculating and explaining the standard deviation and variance.

Comparing Quantities Across Categories

New dataset: Airplane Flights

Which airline carriers are most likely to be delayed?

Let’s look at a data set of all domestic flights that departed from one of New York City’s airports (JFK, LaGuardia, and Newark) on November 16, 2013.

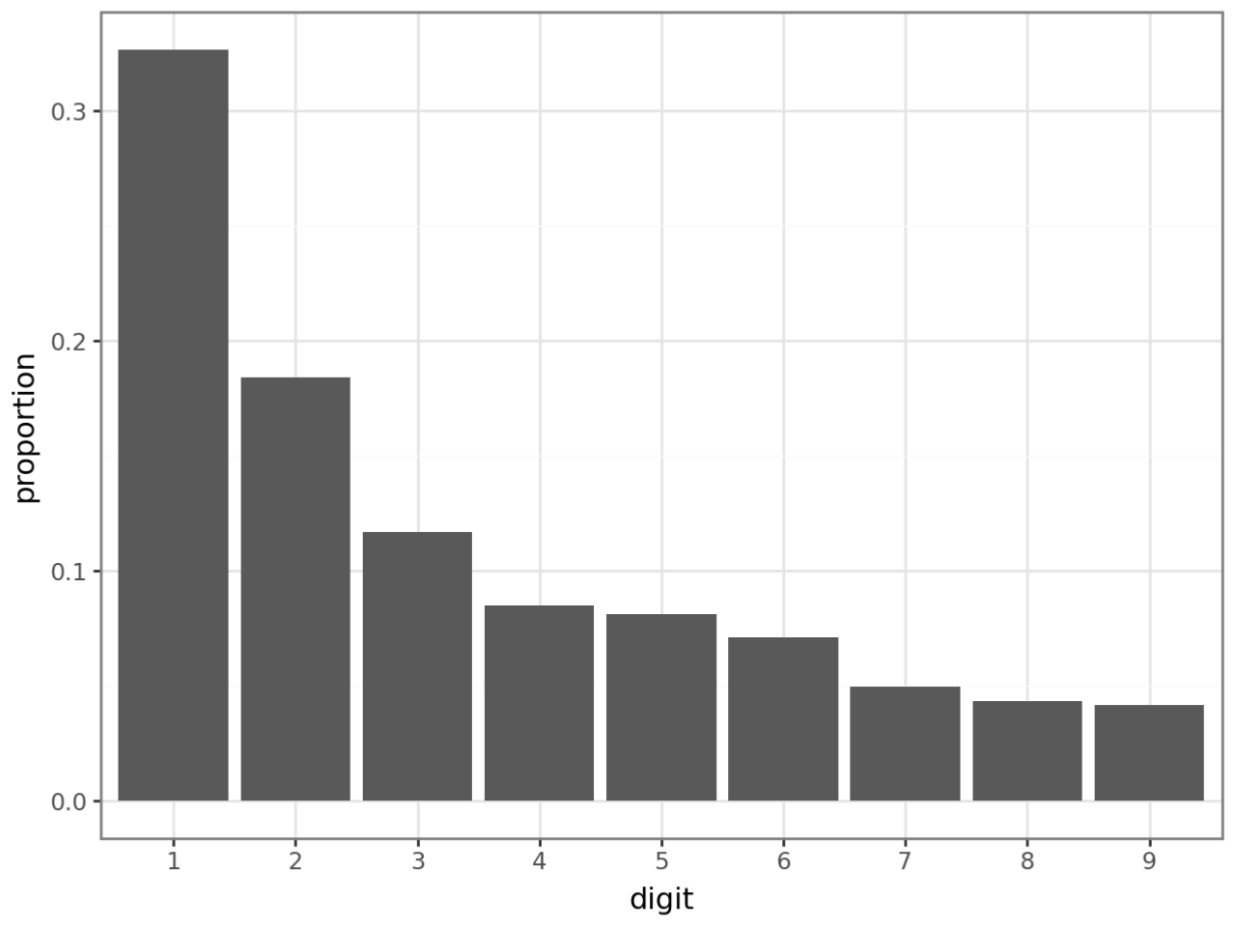
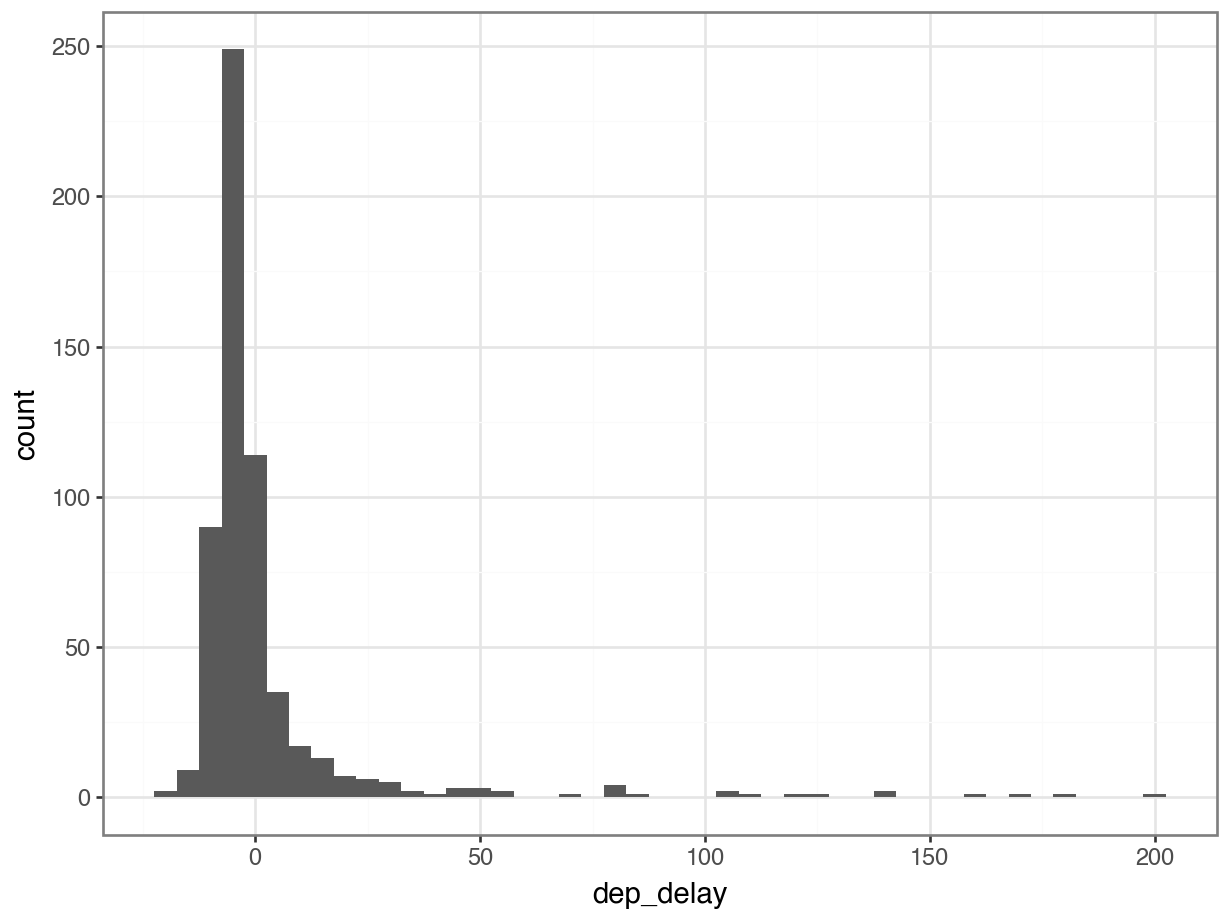
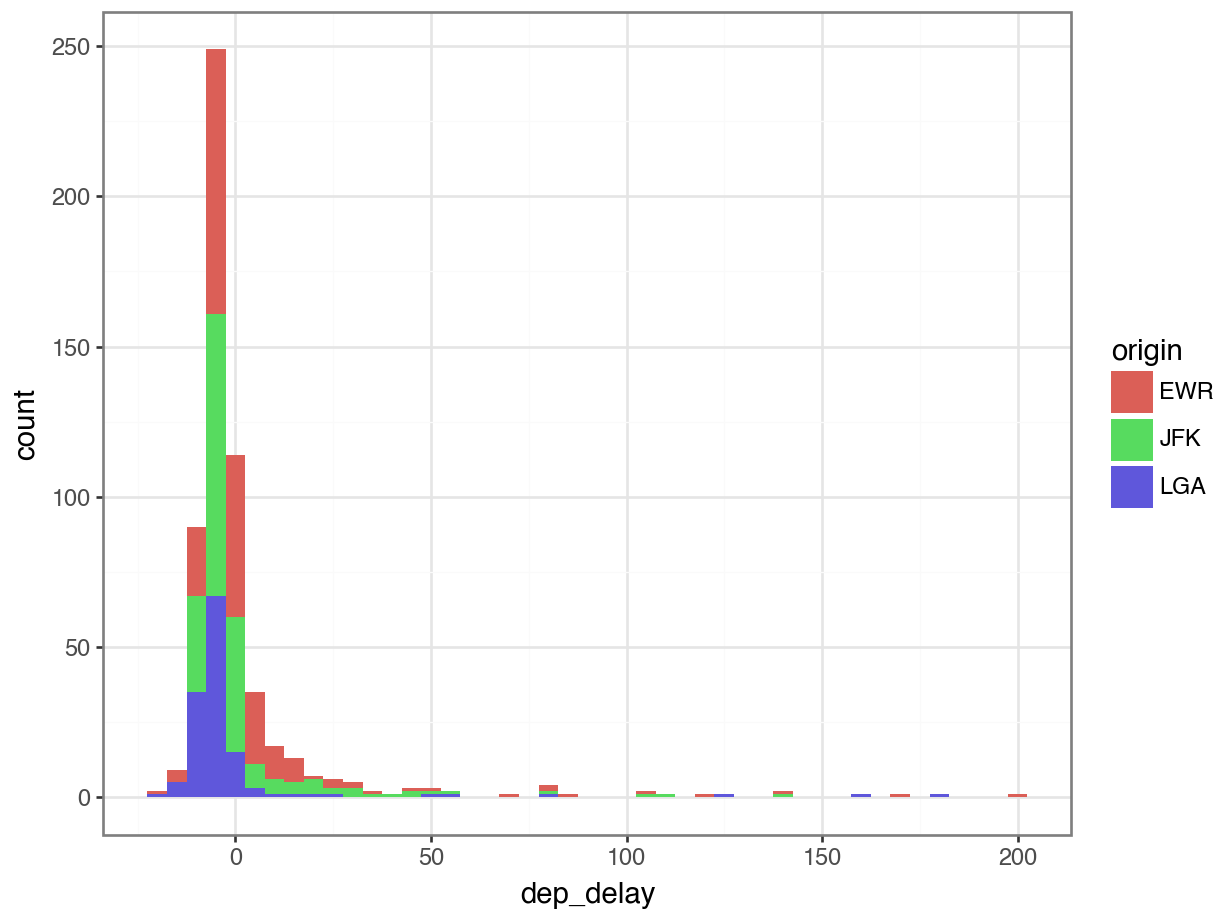
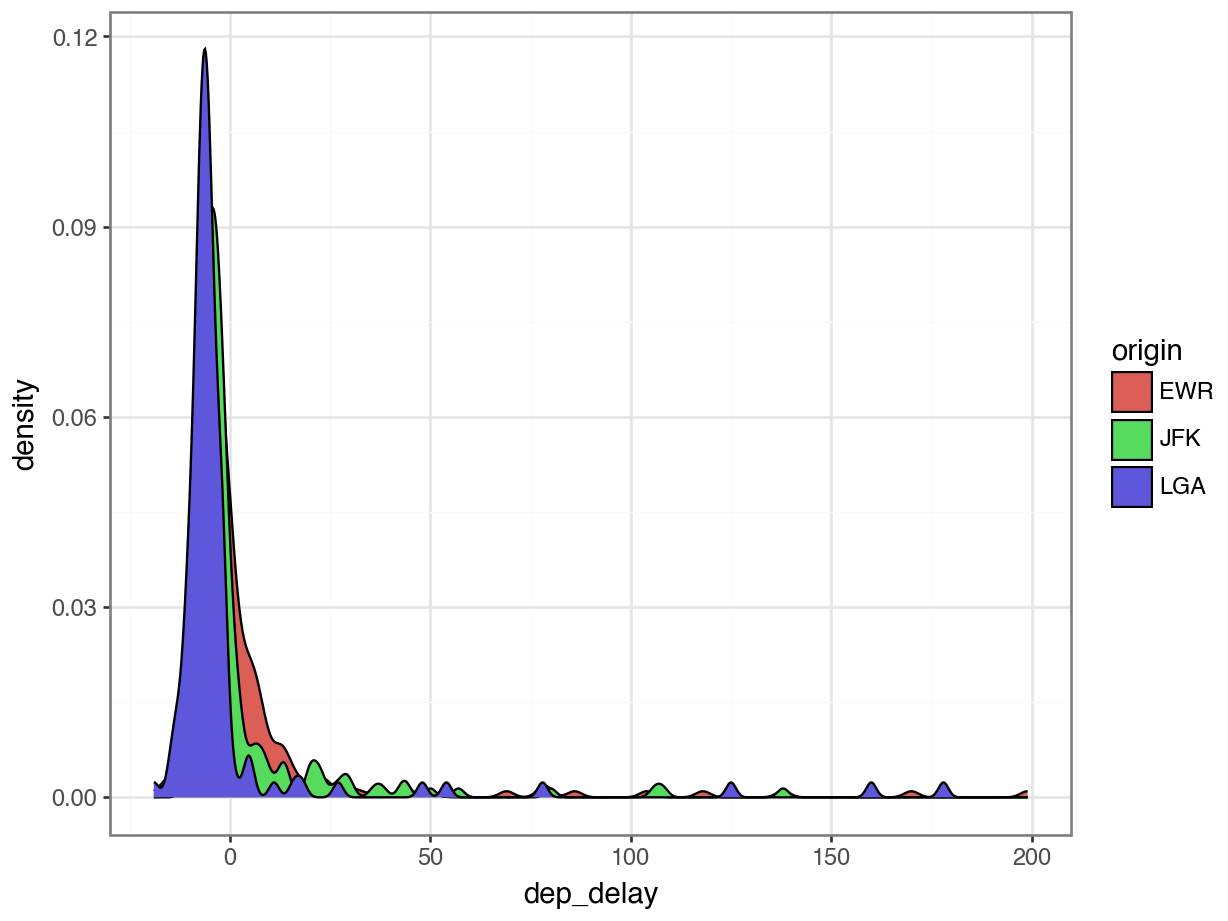
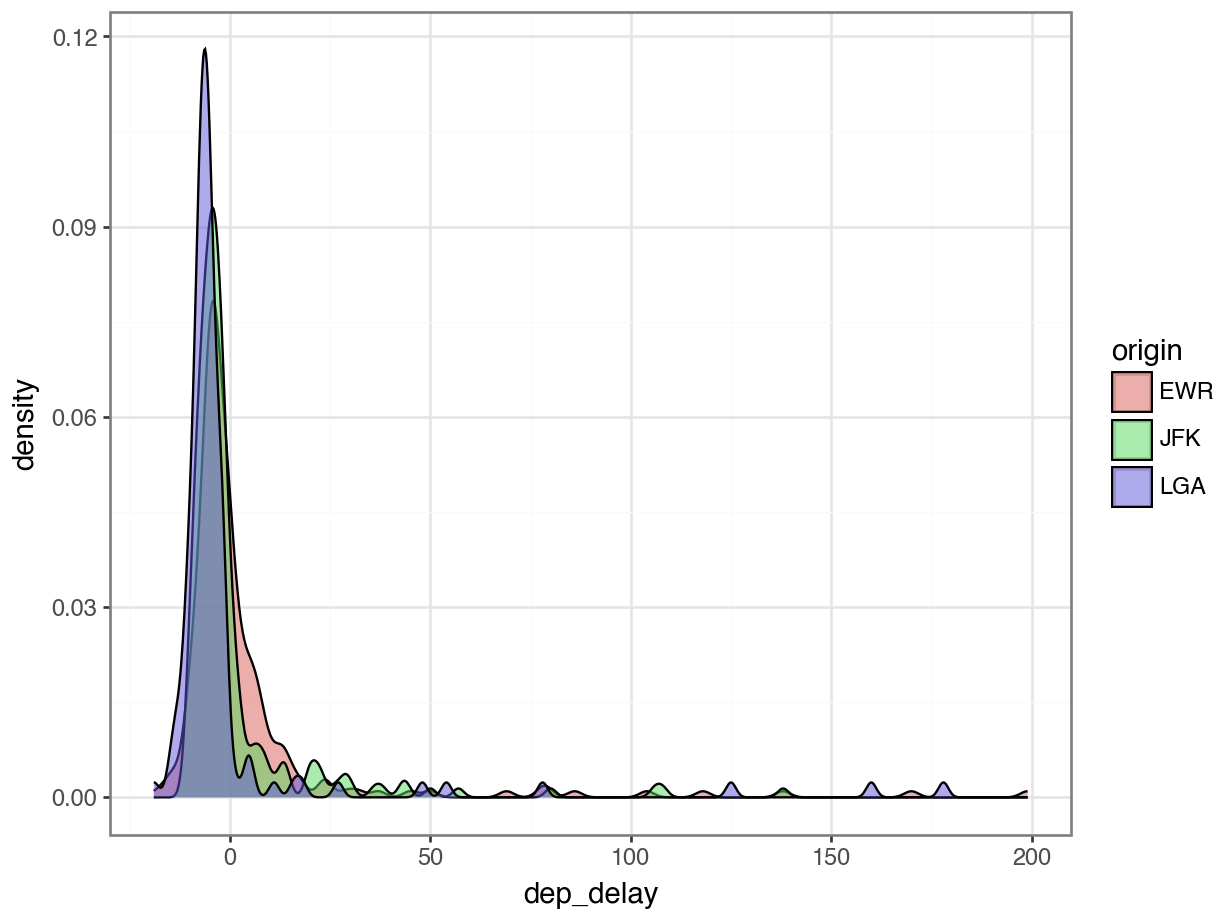
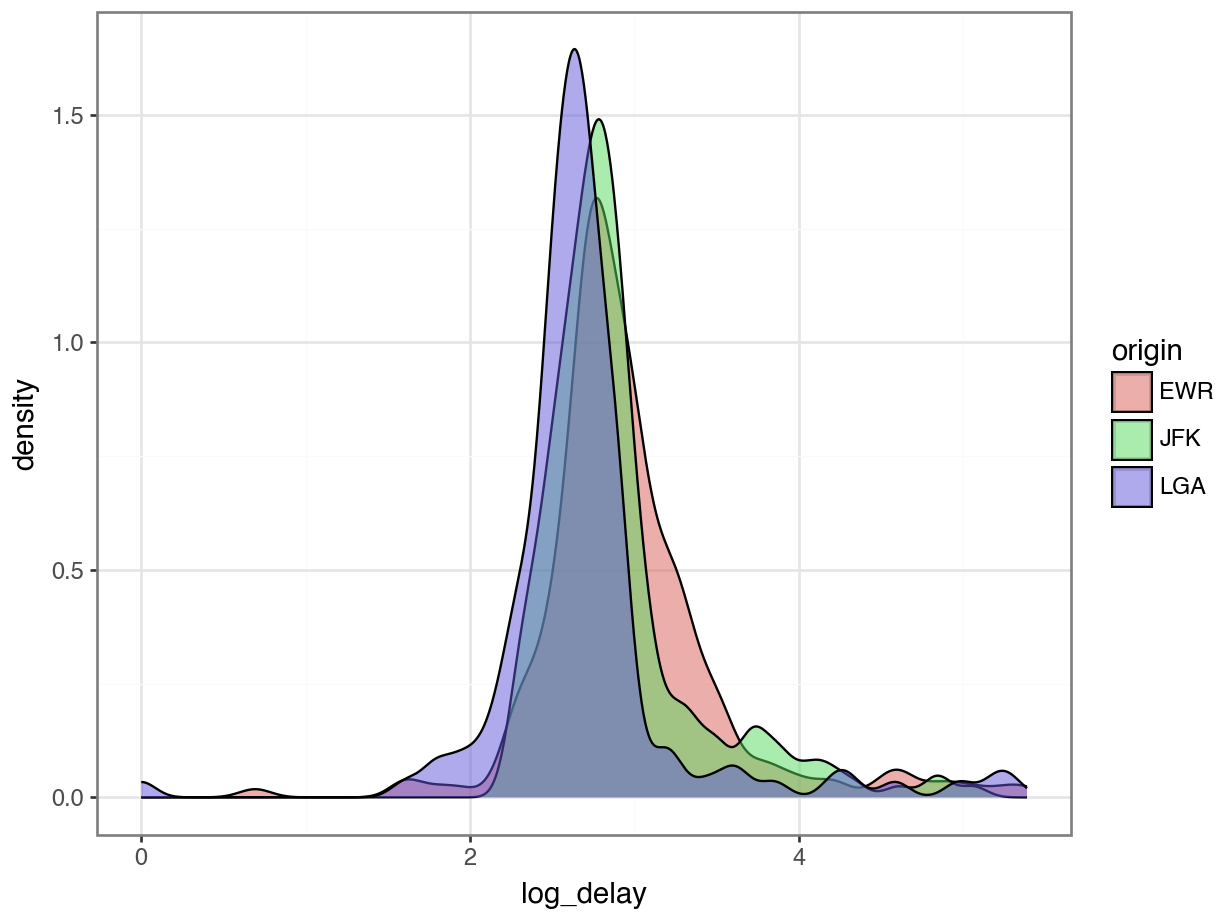
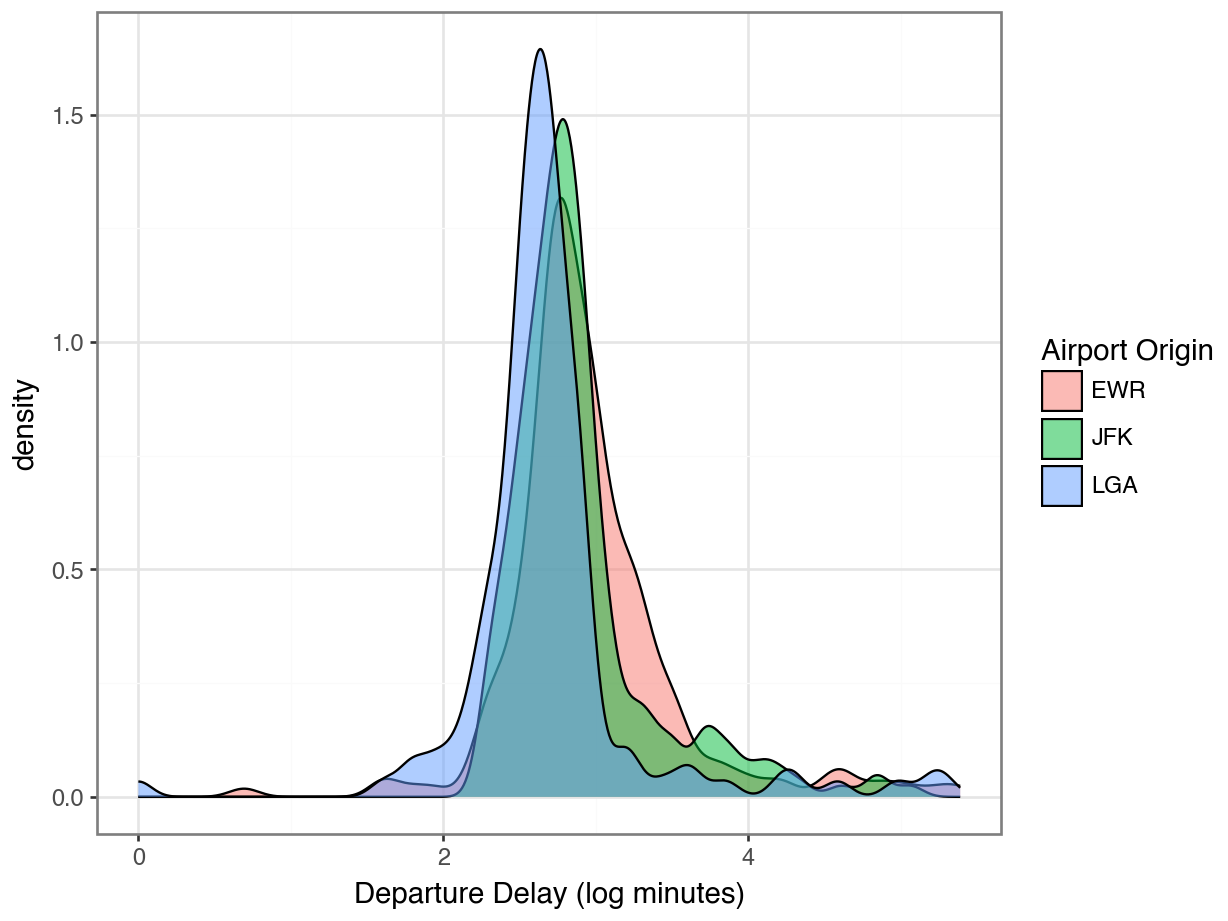
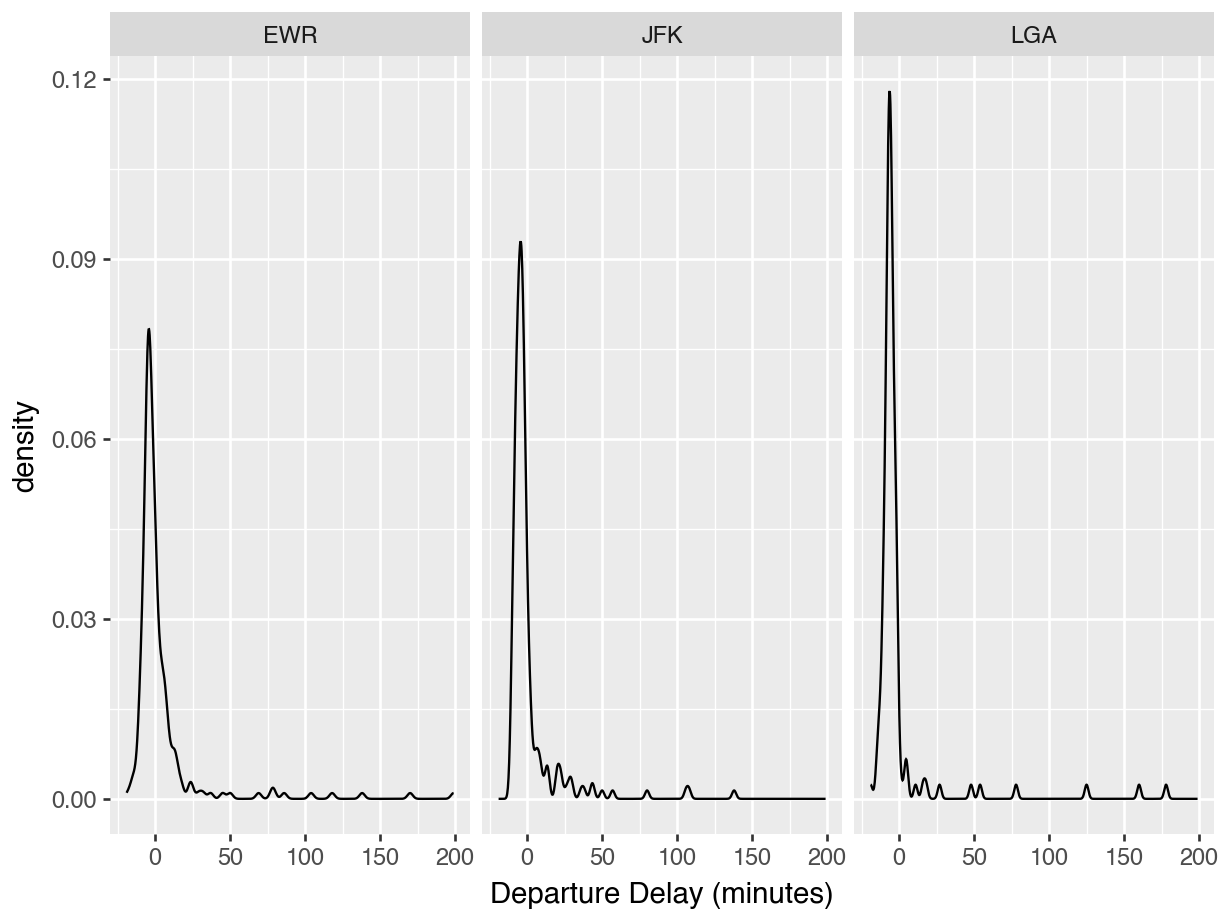
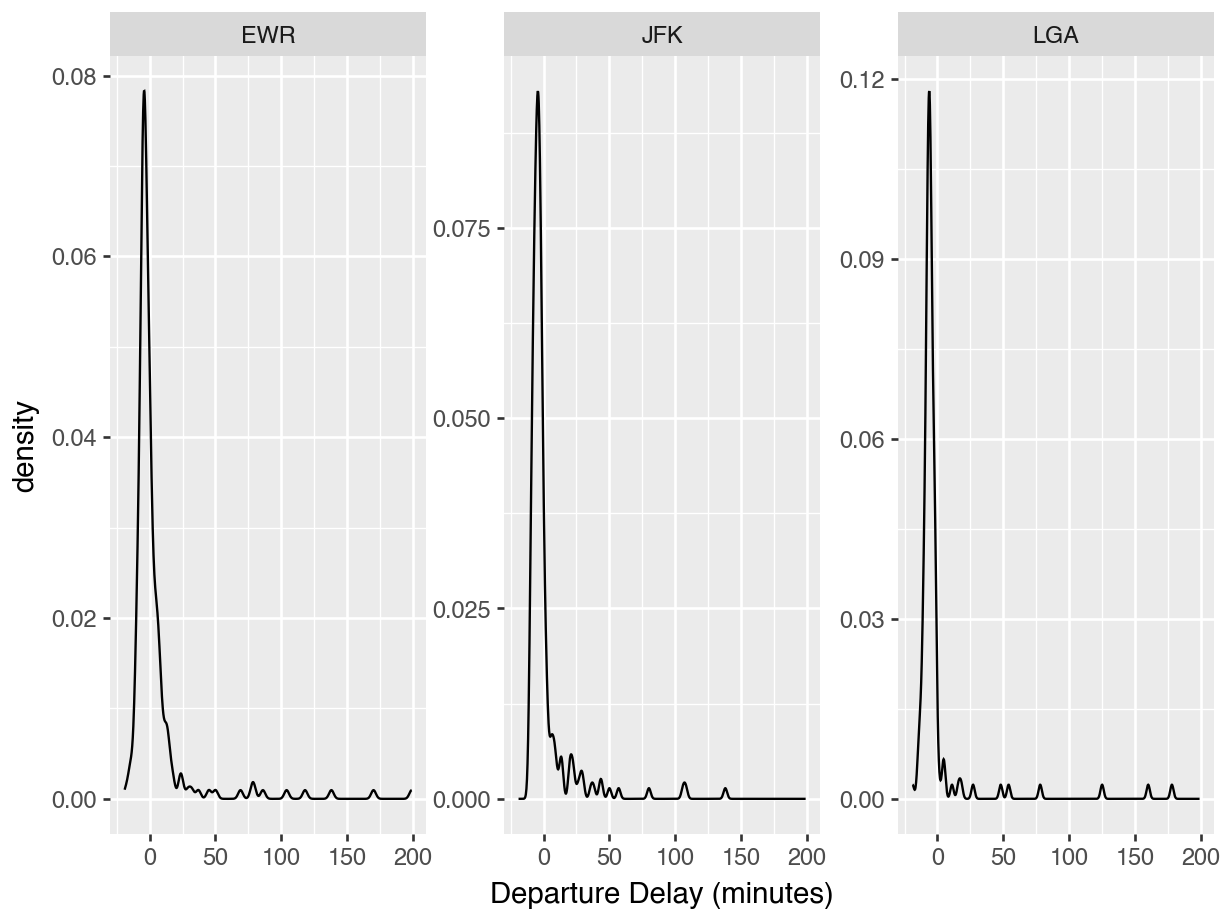
data_dir = "https://datasci112.stanford.edu/data/"
df = pd.read_csv(data_dir + "flights_nyc_20131116.csv")
df

    carrier  flight origin dest  dep_delay
0        US    1895    EWR  CLT       -5.0
1        UA    1014    LGA  IAH       -3.0
2        AA    2243    JFK  MIA        2.0
3        UA     303    JFK  SFO       -8.0
4        US     795    LGA  PHL       -8.0
..      ...     ...    ...  ...        ...
573      B6     745    JFK  PSE       -3.0
574      B6     839    JFK  BQN        0.0
575      UA     360    EWR  PBI        NaN
576      US    1946    EWR  CLT        NaN
577      US    2142    LGA  BOS        NaN

[578 rows x 5 columns]

Delays

We already know how to summarize the flight delays:

Check-in 2.2: Interpret these numbers!

df['dep_delay'].median()

np.float64(-4.0)

df['dep_delay'].mean()

np.float64(2.0469565217391303)

df['dep_delay'].std()

np.float64(23.52882923523891)

Delays

We already know how to visualize the flight delays:

Check-in 2.2: How would you describe this distribution?

Delays by Origin

Do the three origin airports (JFK, LGA, EWR) have different delay patterns?

Check-in 2.2: What could you change in this code to include the origin variable?

(
  ggplot(df, aes(x = 'dep_delay')) + 
  geom_histogram() + 
  theme_bw()
)

Delays by Origin

Overlapping histograms can be really hard to read…

Code

(
  ggplot(df, aes(x = 'dep_delay', fill = 'origin')) + 
  geom_histogram() + 
  theme_bw()
)

Delays by Origin

… but overlapping densities often look nicer…

Code

(
  ggplot(df, aes(x = 'dep_delay', fill = 'origin')) + 
  geom_density() + 
  theme_bw()
)

Delays by Origin

… especially if we make them a little see-through!

Code

(
  ggplot(df, aes(x = 'dep_delay', fill = 'origin')) + 
  geom_density(alpha = 0.5) + 
  theme_bw()
)

Variable Transformations

That last plot was okay, but it was hard to see the details, because the distribution is so skewed right.
Sometimes, for easier visualization, it is worth transforming a variable.
For skewed data, we often use a log transformation.

Log Transformation

Example: Salaries of $10,000, and $100,000, and $10,000,000:

dat = pd.DataFrame({"salary": [10000, 100000, 10000000]})
dat["log_salary"] = np.log(dat["salary"])

Code

(
  ggplot(data = dat, mapping = aes(x = "salary")) + 
  geom_histogram(bins = 100) + 
  theme_bw()
)

Code

(
  ggplot(data = dat, mapping = aes(x = "log_salary")) + 
  geom_histogram(bins = 100) + 
  theme_bw()
)

Log transformations

Usually, we use the natural log, just for convenience.

Pros:

Skewed data looks less skewed, so it is easier to see patterns.

Cons:

The variable is now on a different scale so it is not as interpretable.

Remember, log transformations need positive numbers!

Delays by Origin - Transformed

Code

# Shift delays to be above zero
df['delay_shifted'] = df['dep_delay'] - df['dep_delay'].min() + 1

# Log transform
df['log_delay'] = np.log(df['delay_shifted'])

(
  ggplot(df, aes(x = 'log_delay', fill = 'origin')) + 
  geom_density(alpha = 0.5) + 
  theme_bw()
)

Boxplots

Another option: Boxplots

Code

(
  ggplot(df, mapping = aes(y = 'log_delay', x = 'origin')) + 
  geom_boxplot() + 
  labs(x = "", 
       y = "Log Delay (minutes)", 
       title = "Comparing Departure Delays for NYC Airports") +
  theme_bw()
)

Code

(
  ggplot(df, mapping = aes(y = 'log_delay', x = 'origin')) + 
  geom_boxplot() +
  labs(x = "", 
       y = "Log Delay (minutes)", 
       title = "Comparing Departure Delays for NYC Airports") +
  coord_flip() +
  theme_bw()
)

Facetting

This plot still was a little hard to read.

What if we just made separate plots for each origin?

Separate Plots for Each Origin

One option would be to create separate data frames for each origin.

is_jfk = (df['origin'] == "JFK")
df_jfk = df[is_jfk]
df_jfk

    carrier  flight origin dest  dep_delay  delay_shifted  log_delay
2        AA    2243    JFK  MIA        2.0           22.0   3.091042
3        UA     303    JFK  SFO       -8.0           12.0   2.484907
11       EV    5716    JFK  IAD       -4.0           16.0   2.772589
12       B6     583    JFK  MCO       -3.0           17.0   2.833213
14       B6    1403    JFK  SJU       -2.0           18.0   2.890372
..      ...     ...    ...  ...        ...            ...        ...
570      B6     718    JFK  BOS        1.0           21.0   3.044522
571      B6    1816    JFK  SYR       20.0           40.0   3.688879
572      B6    1503    JFK  SJU      -10.0           10.0   2.302585
573      B6     745    JFK  PSE       -3.0           17.0   2.833213
574      B6     839    JFK  BQN        0.0           20.0   2.995732

[208 rows x 7 columns]

This seems kind of annoying…

FYI: Boolean Masking

How did we filter the previous df to only include "JFK" origins?

Step 1

is_jfk = (df['origin'] == "JFK")
is_jfk

0      False
1      False
2       True
3       True
4      False
       ...  
573     True
574     True
575    False
576    False
577    False
Name: origin, Length: 578, dtype: bool

Step 2

df_jfk = df[is_jfk]
df_jfk["origin"]

2      JFK
3      JFK
11     JFK
12     JFK
14     JFK
      ... 
570    JFK
571    JFK
572    JFK
573    JFK
574    JFK
Name: origin, Length: 208, dtype: object

Facetting

Fortunately, plotnine (and other plotting packages) has a trick for you!

(
  ggplot(df, aes(x = 'dep_delay')) + 
  geom_density() + 
  facet_wrap('origin')
)

Freeing the Scales

Code

(
  ggplot(df, aes(x = 'dep_delay')) + 
  geom_density() + 
  facet_wrap('origin', scales = "free_y") +
  labs(x = "Departure Delay (minutes)")
)

Summaries by Group

Split-apply-combine

Our visualizations told us some of the story, but can we use numeric summaries as well?
To do this, we want to calculate the mean or median delay time for each origin airport.
We call this split-apply-combine:
- split the dataset up by a categorical variable origin
- apply a calculation like mean
- combine the results back into one dataset
In pandas, we use the groupby() function to take care of the split and combine steps!

Group-by

(
  df
  .groupby(by = "origin")["dep_delay"]
  .mean()
)

origin
EWR    4.064935
JFK    1.461538
LGA   -0.485294
Name: dep_delay, dtype: float64

(
  df
  .groupby(by = "origin")["dep_delay"]
  .median()
)

origin
EWR   -3.0
JFK   -4.0
LGA   -6.0
Name: dep_delay, dtype: float64

Group-by Check-in

Check-in 2.2

Which code is causing “split by origin”?
Which code is causing “calculate the mean of delays”?
Which code is causing the re-combining of the data?

(
  df
  .groupby(by = "origin")["dep_delay"]
  .mean()
)

Standardized Values

Simple Example: Exam Scores

Hermione’s exam scores are is:

Potions class: 77/100
Charms class: 95/100
Herbology class: 90/100

In which class did she do best?

But wait!

The class means are:

Potions class: 75/100
Charms class: 85/100
Herbology class: 85/100

In which class did she do best?

But wait!

The class standard deviations are:

Potions class: 2 points
Charms class: 5 points
Herbology class: 1 point

In which class did she do best?

Different variabilities by origin

In addition to having different centers, the three origins also have different spreads.

(
  df
  .groupby("origin")["dep_delay"]
  .std()
)

origin
EWR    25.646258
JFK    18.713927
LGA    26.121365
Name: dep_delay, dtype: float64

In general flights from "LGA" have departure delays that are the furthest from the mean.

Standardized values

We standardize values by subtracting the mean and dividing by the standard deviation.
This tells us how much better/worse than typical values our target value is.
This is also called the z-score. \[z_i = \frac{x_i - \bar{x}}{s_x}\]

Standardized values

Suppose you fly from LGA and your flight is 40 minutes late. Your friend flies from JFK and their flight is 30 minutes late.

Who got “unluckier”?

You?

(40 - -0.48) / 26.12

1.5497702909647777

Your friend?

(30 - 1.46) / 18.71

1.5253874933190805

Activity 2.2

Do the different airlines have different patterns of flight delays?

Make a plot to answer the question.
Calculate values to answer the question.
The first row is a flight from EWR to CLT on US Airways. The second row is a flight from LGA to IAH on United Airlines. Which one was a “more extreme” delay?

Relationships Between Quantitative Variables

Did older passengers pay a higher fare on the Titanic?

To visualize two quantitative variables, we make a scatterplot (or point geometry).

Code

(
  ggplot(data = df_titanic, mapping = aes(x = 'age', y = 'fare')) + 
  geom_point() +
  labs(x = "Age of Passenger", 
       y = "Fare Paid on Titanic")
)

Scatterplots

Notice

The explanatory variable was on the x-axis.
The response variable was on the y-axis.
“If you are older, you pay more” not “If you pay more, you get older”.

(
  ggplot(data = df_titanic, 
         mapping = aes(x = 'age', y = 'fare')
         ) + 
  geom_point() +
  labs(x = "Age of Passenger", 
       y = "Fare Paid on Titanic")
)

Making a Clearer Plot

Did you notice how difficult it was to pick out each point?

Point Size

Code

(
  ggplot(data = df_titanic, 
         mapping = aes(x = 'age', y = 'fare')
         ) + 
  geom_jitter(size = 0.5) +
  labs(x = "Age of Passenger", 
       y = "Fare Paid on Titanic")
)

Transparency

Code

(
  ggplot(data = df_titanic, 
         mapping = aes(x = 'age', y = 'fare')
         ) + 
  geom_point(alpha = 0.5) +
  labs(x = "Age of Passenger", 
       y = "Fare Paid on Titanic")
)

Spicing Things Up

How could we make this more interesting?

Use a log-transformation for fare because it is very skewed.
Add in a third variable, pclass. How might you do this?

Challenge

Can you re-create this plot?

Describing a Scatterplot

Let’s look at just third class:

Code

is_third= df_titanic['pclass'] == 3
df_third = df_titanic[is_third]

(
  ggplot(df_third, aes(x = 'age', y = 'fare')) + 
  geom_jitter(alpha = 0.8) + 
  theme_bw()
)

Describing the Relationship

Strength

Not very strong: the points don’t follow a clear pattern.

Direction

Slightly negative: When age was higher, fare was a little lower.

Shape

Not very linear: the points don’t form a straight line.

Correlation

What if we want a numerical summary of the relationship between variables?

Do “older than average” people pay “higher than average” fares?
- In other words, when the z-score of age was high, was the z-score of fare also high?

Age & Fare Correlation

Code

mean_age = df_third['age'].mean()
mean_fare = df_third['fare'].mean()

(
  ggplot(data = df_third, mapping = aes(x = 'age', y = 'fare')) + 
  geom_jitter(alpha = 0.8) + 
  geom_vline(xintercept = mean_age, color = "red", linetype = "dashed") + 
  geom_hline(yintercept = mean_fare, color = "red", linetype = "dashed") + 
  labs(x = "Age of Passenger", 
       y = "Titanic Fare Paid")
  theme_bw()
)

Correlation

Interpret this result:

df_third[['age', 'fare']].corr()

           age      fare
age   1.000000 -0.238137
fare -0.238137  1.000000

Age and fare are slightly negatively correlated.

Can you think of an explanation for this?

Correlation is not the Relationship

The image contains a 3x7 grid of scatterplots illustrating varying correlation patterns. Each scatterplot is labeled with its respective correlation coefficient. The first row demonstrates linear correlations ranging from a perfect positive correlation (1.0) to a perfect negative correlation (-1.0) in decrements of 0.2. The scatterplots show the corresponding transition from a tight upward-sloping line (1.0) to a tight downward-sloping line (-1.0), with increasing dispersion at intermediate values. The second row depicts perfect positive and negative correlations (1.0 and -1.0) represented by straight lines, while the others in the row maintain similar relationships. The third row shows scatterplots with non-linear or no correlation, all labeled as 0. These include distinct shapes like a sine wave, diamond, parabola, hourglass, circle, and clustered points. These shapes demonstrate the absence of linear relationships despite structured patterns.

Just for fun: Guess the Correlation Game

Takeaways

Plot quantitative variables across groups with overlapping density plots, boxplots, or by facetting.
Summarize quantitative variables across groups by using groupby() and then calculating summary statistics.
Know what split-apply-combine means.
Plot relationships between quantitative variables with a scatterplot.
Describe the strength, direction, and shape of the relationship displayed in a scatterplot.
Summarize relationships between quantitative variables with the correlation