Visualizing and Summarizing Quantitative Variables

Some Class Updates!

Changes from Week 1

Week 1 taught me that I need to make some adjustments!

Lab Attendance

Is not required. However, if you do not attend lab and come to student hours or post questions on Discord about the lab, I will be displeased.

Deadlines

Labs will be due the day after lab.

• Tuesday’s lab is due on Wednesday at 11:59pm.
• Thursday’s lab is due on Friday at 11:59pm.

Quizzes from the lecture slides are due by 11:59pm that night.

Lab Activities

I’m going to do my best to ensure all the skills necessary to complete the lab activities are covered during lecture.

The story so far…

Getting, prepping, and summarizing data

titanic = pd.read_csv("data/titanic.csv")

titanic["Pclass"] = titanic["Pclass"].astype("category")
titanic["Survived"] = titanic["Survived"].astype("category")

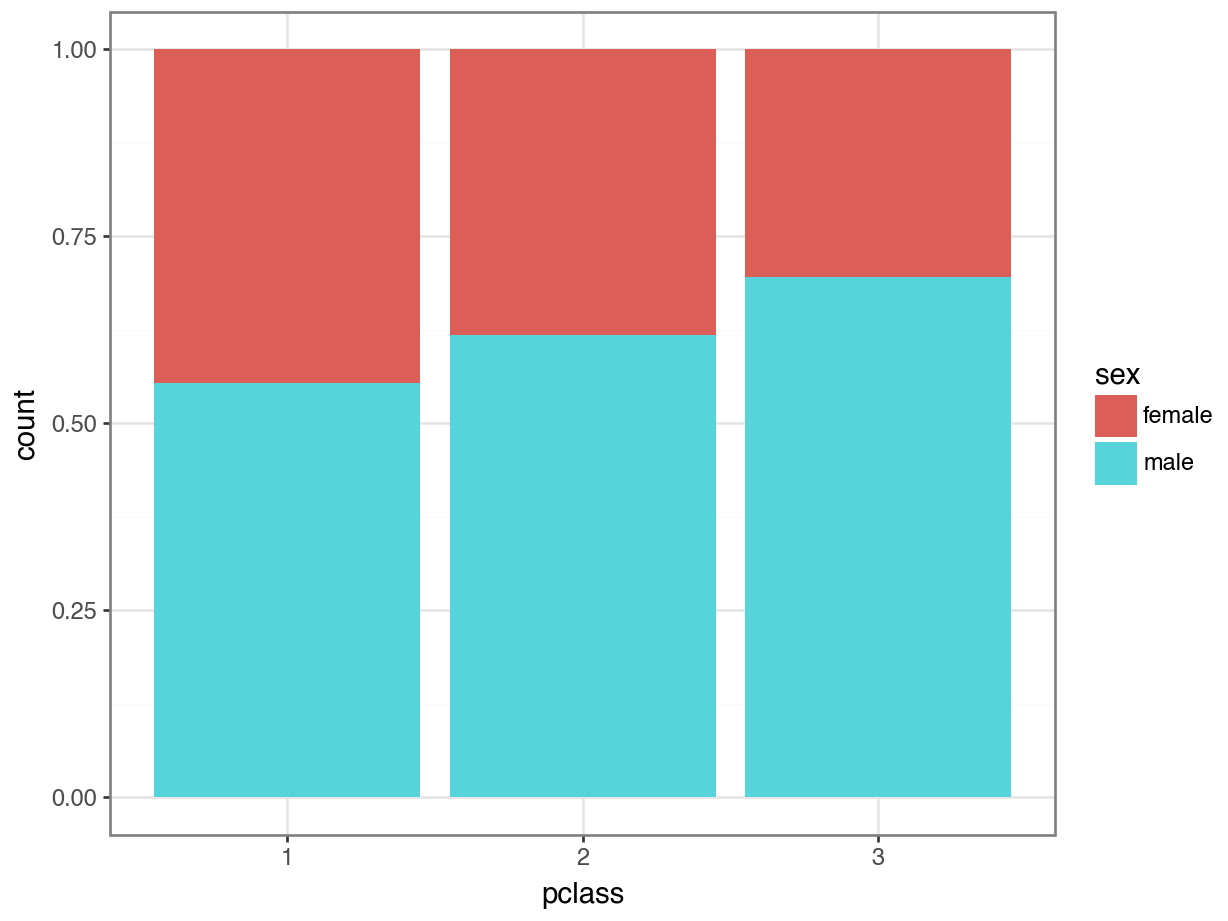
Marginal Distributions

If I choose a passenger at random, what is the probability they rode in 1st class?

marginal_class = (
  titanic['Pclass']
  .value_counts(normalize = True)
  )
marginal_class

Pclass
3    0.551066
1    0.242424
2    0.206510
Name: proportion, dtype: float64

Joint Distributions

If I choose a passenger at random, what is the probability they are a woman who rode in first class?

joint_class_sex = (
  titanic[["Pclass", "Sex"]]
  .value_counts(normalize=True)
  .unstack()
  )
  
joint_class_sex

Sex       female      male
Pclass                    
1       0.105499  0.136925
2       0.085297  0.121212
3       0.161616  0.389450

Conditional Distributions

If I choose a woman at random, what is the probability they rode in first class?

marginal_sex = (
  titanic['Sex']
  .value_counts(normalize = True)
  )
  
joint_class_sex.divide(marginal_sex)

Sex       female      male
Pclass                    
1       0.299363  0.211438
2       0.242038  0.187175
3       0.458599  0.601386

Visualizing with plotnine

(
  ggplot(data = titanic, aes(x = "Sex", fill = "Pclass")) + 
  geom_bar(position = "fill") + 
  theme_bw()
)

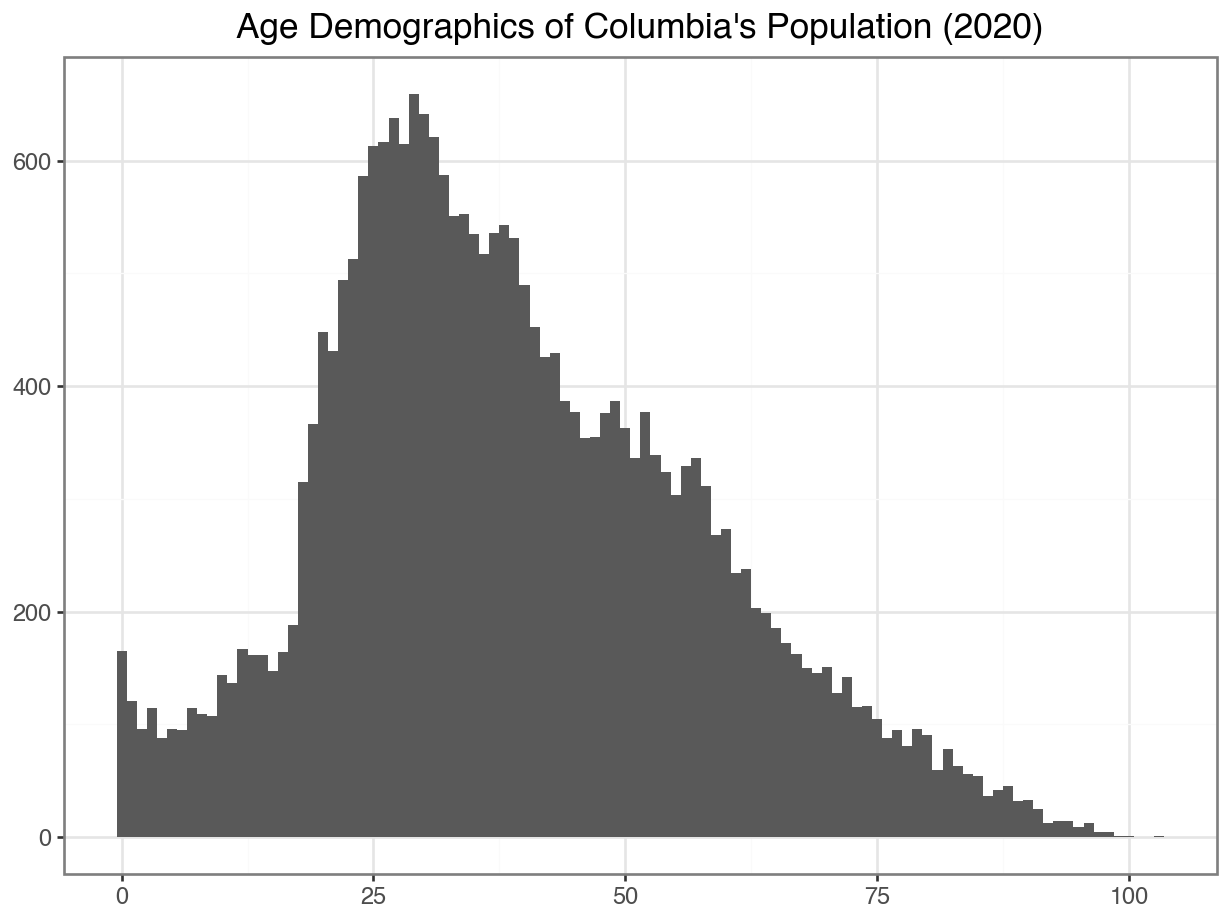
Quantitative Variables

We have already analyzed a quantitative variable in the COVID data!

Visualizing One Quantitative Variable

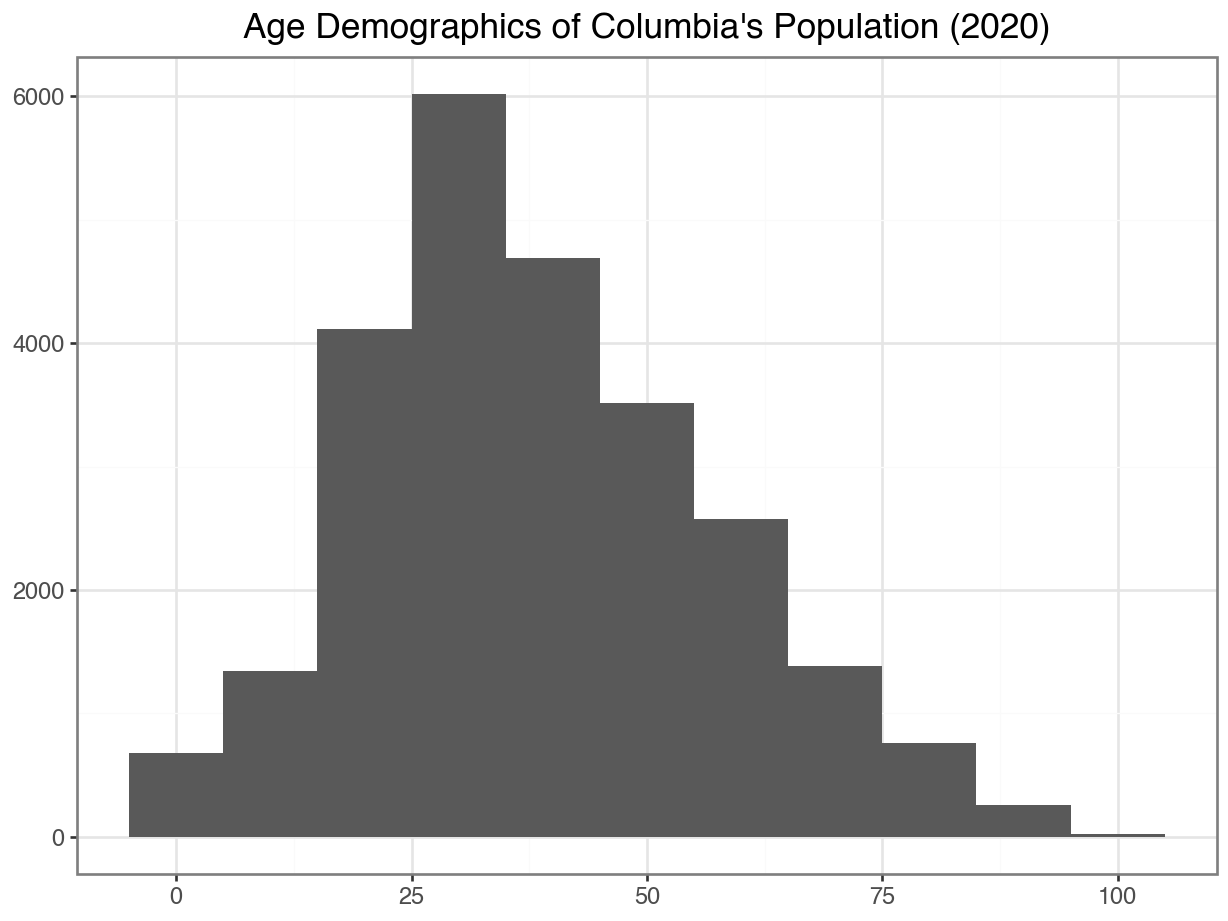
Option 1: Convert it to categorical

To visualize the age variable, we did the following:

df_CO["age"] = pd.cut(
    df_CO["Edad"],
    bins = [0, 10, 20, 30, 40, 50, 60, 70, 80, 120],
    labels = ["0-9", "10-19", "20-29", "30-39", "40-49", "50-59", "60-69", "70-79", "80+"],
    right = False, 
    ordered = True)
    

Option 1: Then make a barplot

Then, we could treat age as categorical and make a barplot:

(
  ggplot(data = df_CO, mapping = aes(x = "age")) + 
  geom_bar() + 
  labs(x = "", 
       y = "", 
       title = "Age Demographics of Columbia's Population (2020)"
       ) +
  theme_bw() 
)

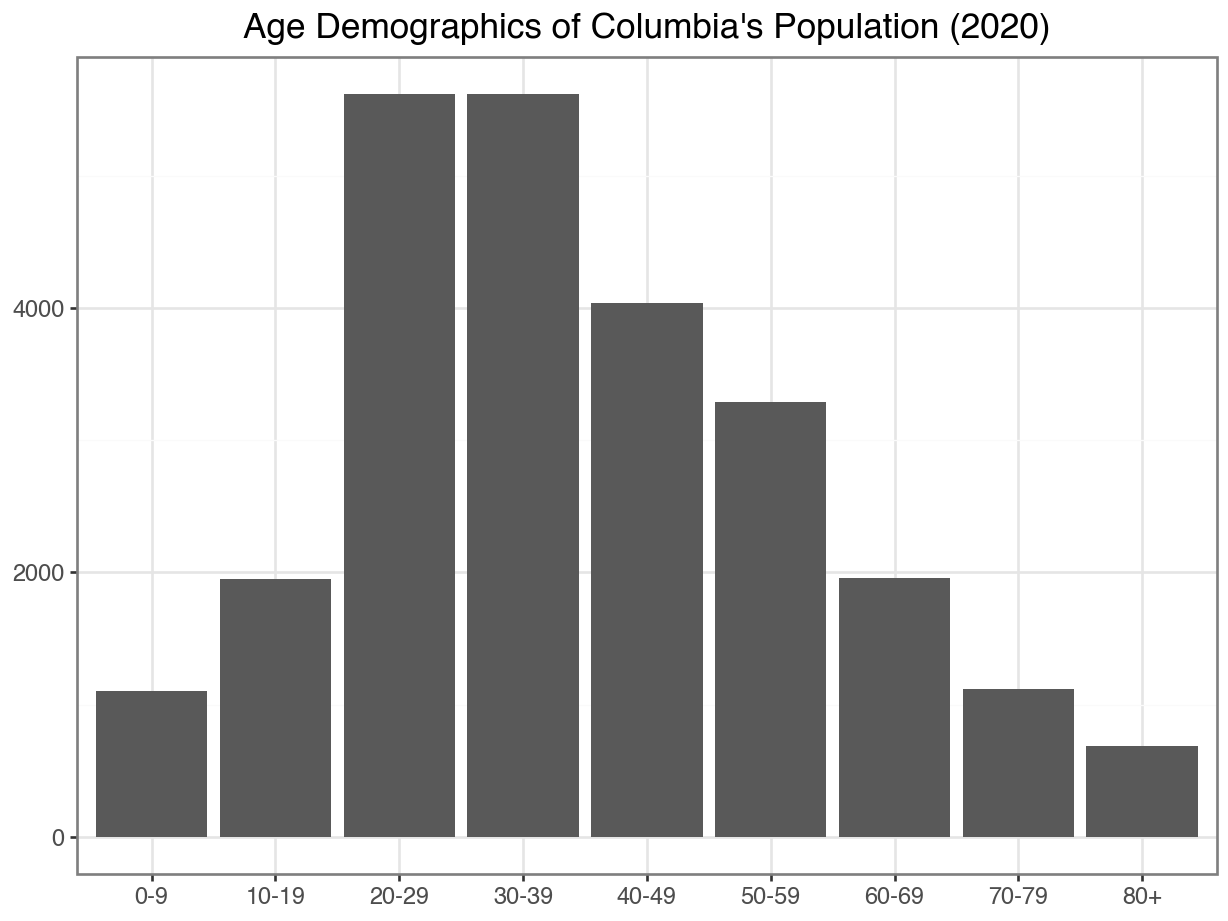
But this process seems a bit odd…

Option 2: Treat it as a quantitative variable!

A histogram uses equal sized bins to summarize a quantitative variable.

(
  ggplot(data = df_CO, mapping = aes(x = "Edad")) + 
  geom_histogram() + 
  labs(x = "", 
       y = "", 
       title = "Age Demographics of Columbia's Population (2020)"
       ) +
  theme_bw()
)

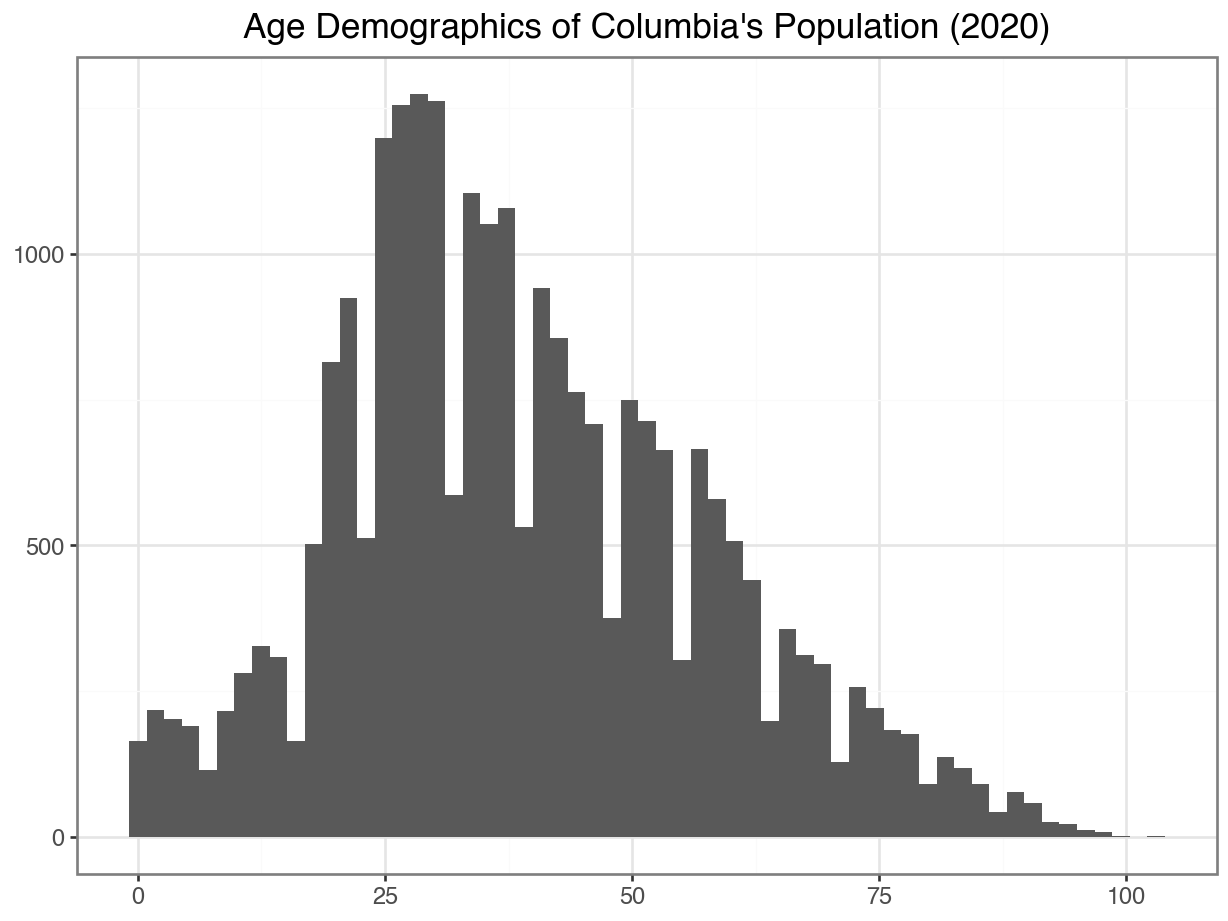
Adding Style to Your Histogram

Changing Binwidth

To tweak your histogram, you can change the binwith:

(
  ggplot(data =df_CO, mapping = aes(x = "Edad")) + 
  geom_histogram(binwidth = 1) + 
  labs(x = "", 
       y = "", 
       title = "Age Demographics of Columbia's Population (2020)"
       ) +
  theme_bw()
)

(
  ggplot(data =df_CO, mapping = aes(x = "Edad")) + 
  geom_histogram(binwidth = 10) + 
  labs(x = "", 
       y = "", 
       title = "Age Demographics of Columbia's Population (2020)"
       ) +
  theme_bw()
)

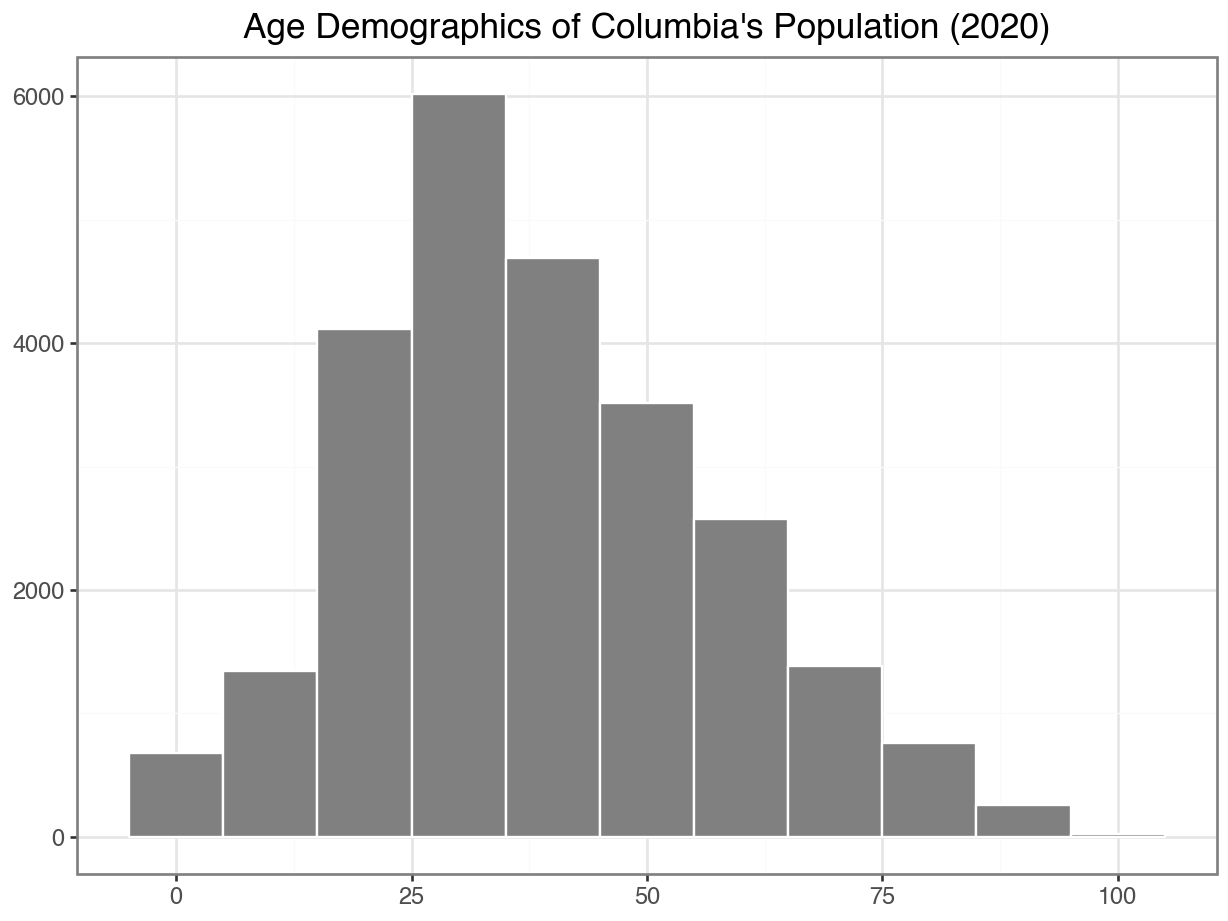
Adding Color & Outline

(
  ggplot(data =df_CO, mapping = aes(x = "Edad")) + 
  geom_histogram(binwidth = 10, 
                 color = "orange", 
                 fill = "darkgray") + 
  labs(x = "", 
       y = "", 
       title = "Age Demographics of Columbia's Population (2020)"
       ) +
  theme_bw()
)

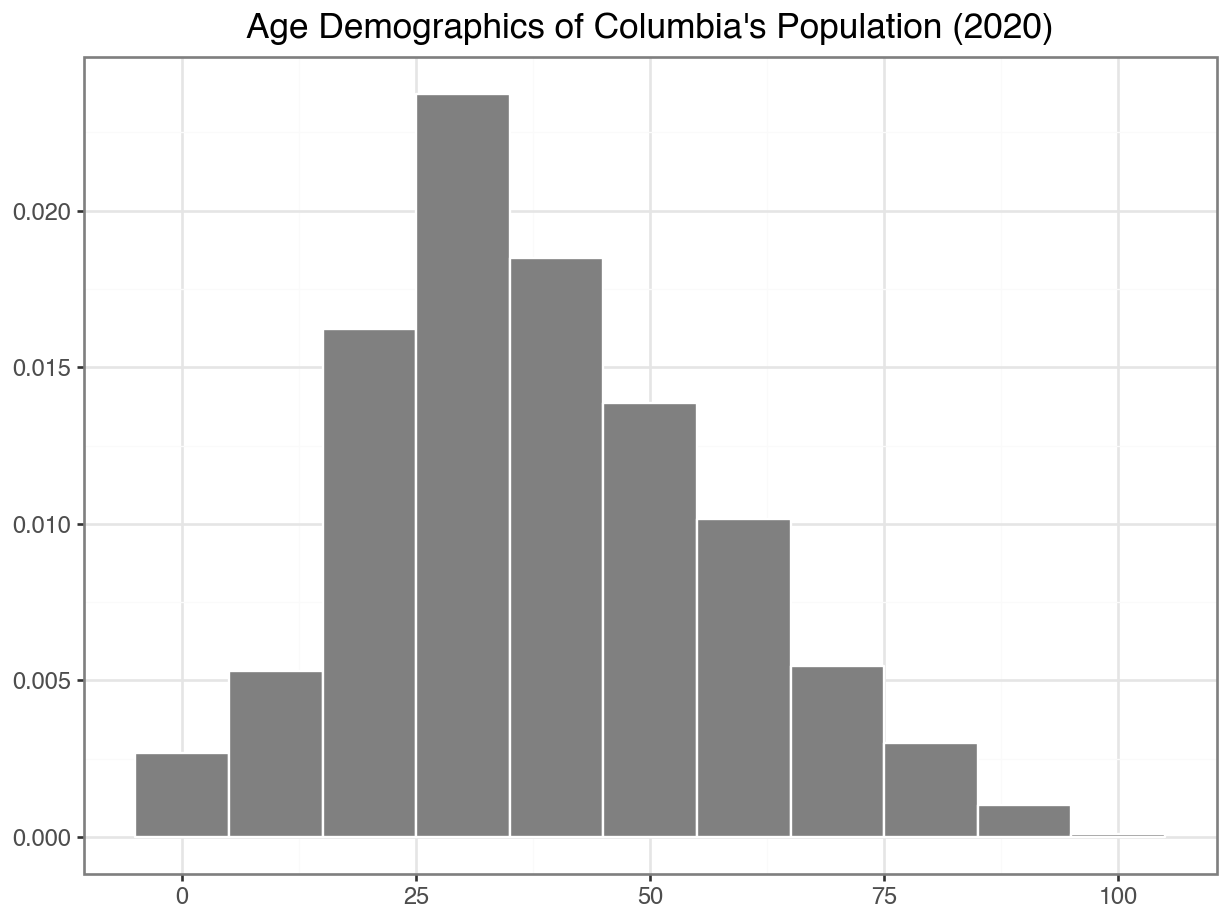
Using Percents Instead of Counts

(
  ggplot(data =df_CO, mapping = aes(x = "Edad")) + 
  geom_histogram(mapping = aes(y = '..density..'), 
                 binwidth = 10, 
                 color = "orange", 
                 fill = "darkgray") + 
  labs(x = "", 
       y = "", 
       title = "Age Demographics of Columbia's Population (2020)"
       ) +
  theme_bw()
)

Distributions

• Recall the distribution of a categorical variable:

  • What are the possible values and how common is each?

• The distribution of a quantitative variable is similar:

  • The total area in the histogram is 1.0 (or 100%).

Densities

• In this example, we have a limited set of possible values for age: 0, 1, 2, …., 100.

  • We call this a discrete variable.

• What if had a quantitative variable with infinite values?

  • For example: Price of a ticket on Titanic.
  • We call this a continuous variable.

• In this case, it is not possible to list all possible values and how likely each one is.
  • One person paid $2.35
  • Two people paid $12.50
  • One person paid $34.98
  • \(\vdots\)

• Instead, we talk about ranges of values.

Densities

About what percent of people in this dataset are below 18?

(
  ggplot(data = df_CO, mapping = aes(x = "Edad")) + 
  geom_histogram(mapping = aes(y = '..density..'), 
                 bins = 10, 
                 color = "orange", 
                 fill = "darkgray") + 
  geom_vline(xintercept = 18, 
             color = "red", 
             size = 2, 
             linetype = "dashed") +
  theme_bw()
)

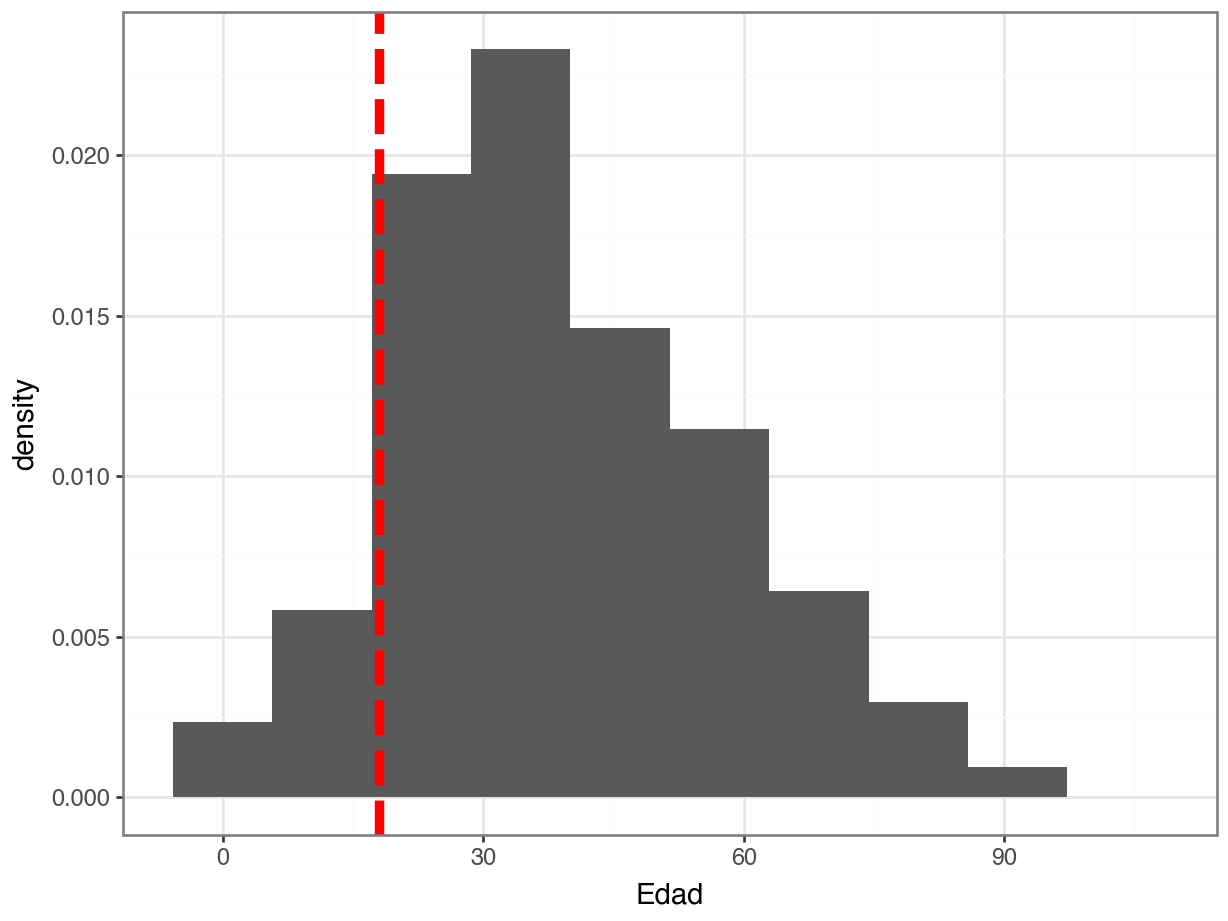
How would you code it?

Summarizing One Quantitative Variable

df_CO['Edad']

0        19
1        34
2        50
3        55
4        25
         ..
25361    48
25362    55
25363    39
25364    13
25365     0
Name: Edad, Length: 25366, dtype: int64

If you had to summarize this variable with one single number, what would you pick?

Summaries of Center: Mean

Mean

• One summary of the center of a quantitative variable is the mean.

• When you hear “The average age is…” or the “The average income is…”, this probably refers to the mean.

• Suppose we have five people, ages: 4, 84, 12, 27, 7

• The mean age is: \[(4 + 84 + 12 + 27 + 7) / 5 = 134 / 5 = 26.8\]

Notation Interlude

• To refer to our data without having to list all the numbers, we use \(x_1, x_2, ..., x_n\)

• In the previous example, \(x_1 = 4, x_2 = 84, x_3 = 12, x_4 = 27, x_5 = 7\). So, \(n = 5\).

• To add up all the numbers, we use the summation notation: \[ \sum_{i = 1}^5 x_i = 134\]

• Therefore, the mean is: \[\bar{x} = \frac{1}{n} \sum_{i = 1}^n x_i\]

Means in Python

Long version: find the sum and the number of observations

sum_age = df_CO["Edad"].sum()
n = len(df_CO)

sum_age / n

np.float64(39.04742568792872)

Short version: use the built-in .mean() function!

df_CO["Edad"].mean()

np.float64(39.04742568792872)

Activity 2.1

The mean is only one option for summarizing the center of a quantitative variable. It isn’t perfect!

Let’s investigate this.

• Open the Activity 2.1 Collab notebook

• Read in the Titanic data

• Plot the density of ticket prices on titanic

• Calculate the mean price

• See how many people paid more than mean price

What happened

• Our fare data was skewed right: Most values were small, but a few values were very large.

• These large values “pull” the mean up; just how the value 84 pulled the average age up in our previous example.

• So, why do we like the mean?

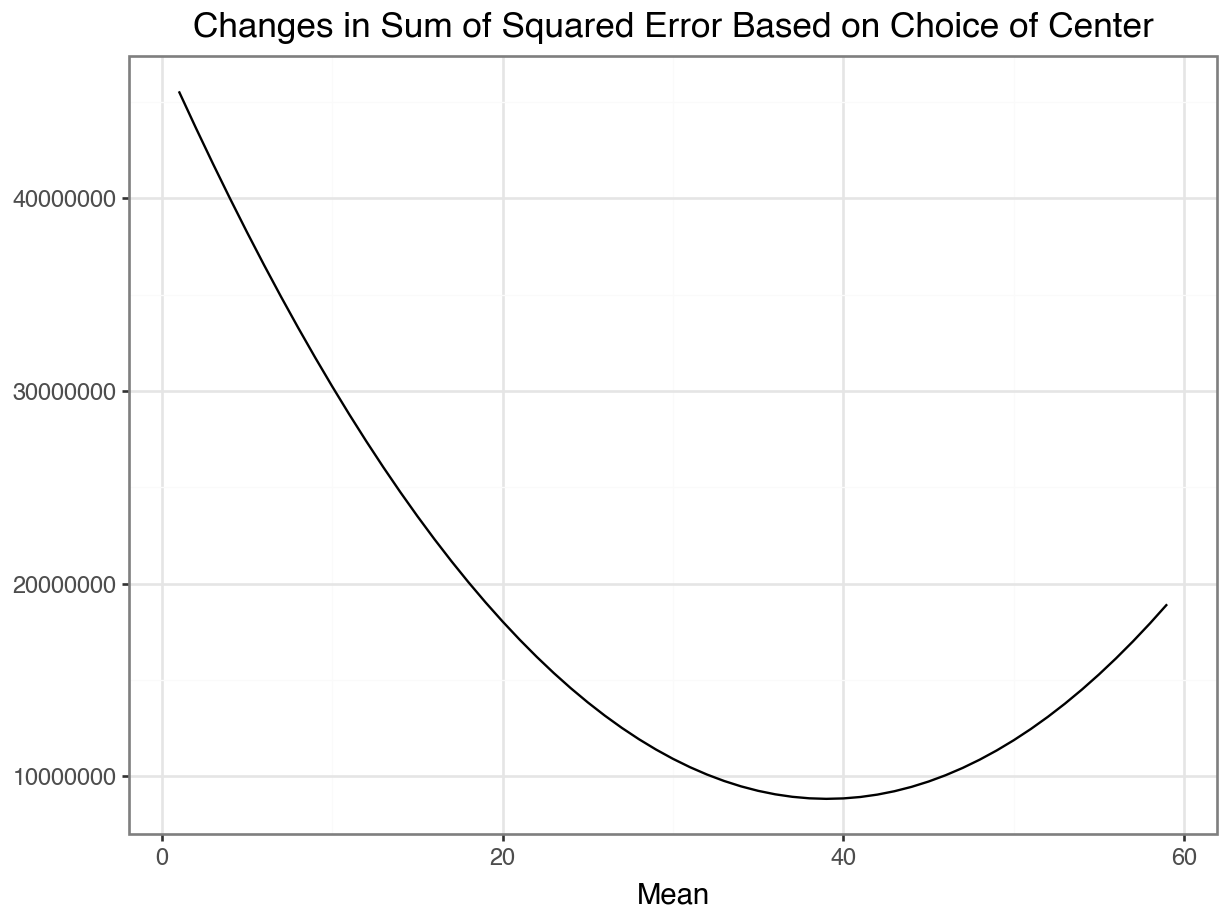
Squared Error

• Recall: Ages 4, 84, 12, 27, 7.

ages = np.array([4, 84, 12, 27, 7])

• Imagine that we had to “guess” the age of the next person.

• If we guess 26.8, then our “squared error” for these five people is:

sq_error = (ages - 26.8) ** 2

(
  sq_error
  .round(decimals = 1)
  .sum()
  )

np.float64(4402.6)

• If we guess 20, then our “squared error” for these five people is:

sq_error = (ages - 20) ** 2
(
  sq_error
  .round(decimals = 1)
  .sum()
  )

np.int64(4634)

Minimizing squared error

cs = range(1, 60)
sum_squared_distances = []

for c in cs:
  (
    sum_squared_distances
    .append(
      (
        (df_CO["Edad"] - c) ** 2
      )
      .sum()
      )

res_df = pd.DataFrame({"center": cs, "sq_error": sum_squared_distances})

(
  ggplot(res_df, aes(x = 'center', y = 'sq_error')) + 
  geom_line() +
  labs(x = "Mean", 
       y = "", 
       title = "Changes in Sum of Squared Error Based on Choice of Center") +
  theme_bw()
  )

Summaries of Center: Median

Median

Another summary of center is the median, which is the “middle” of the sorted values.

To calculate the median of a quantitative variable with values \(x_1, x_2, x_3, ..., x_n\), we do the following steps:

1. Sort the values from smallest to largest: \[x_{(1)}, x_{(2)}, x_{(3)}, ..., x_{(n)}.\]

2. The “middle” value depends on whether we have an odd or an even number of observations.

   • If \(n\) is odd, then the middle value is \(x_{(\frac{n + 1}{2})}\).

   • If \(n\) is even, then there are two middle values, \(x_{(\frac{n}{2})}\) and \(x_{(\frac{n}{2} + 1)}\).

Note

It is conventional to report the mean of the two values (but you can actually pick any value between them)!

Median in Python

Ages: 4, 84, 12, 7, 27. What is the median?

Median age in the Columbia data:

df_CO["Edad"].median()

np.float64(37.0)

Summaries of Spread: Variance

Variance

• One measure of spread is the variance.

• The variance of a variable whose values are \(x_1, x_2, x_3, ..., x_n\) is calculated using the formula \[\textrm{var(X)} = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n - 1}\]

Does this look familiar?

It’s the sum of squared error! Well, divided by \(n-1\), the “degrees of freedom”.

Variance in Python

Similar to calculating the mean, we could find the variance manually:

(
  ((df_CO["Edad"] - df_CO["Edad"].mean()) ** 2)
  .sum() / (len(df_CO) - 1)
  )

np.float64(348.0870469898451)

…or using a built-in Python function.

df_CO["Edad"].var()

np.float64(348.0870469898451)

Standard Deviation

• Notice that the variance isn’t very intuitive. What do we mean by “The spread is 348”?

• This is because it is the squared error!

• To get it in more interpretable language, we can take the square root:

np.sqrt(df_CO["Edad"].var())

np.float64(18.65709106452142)

Or, we use the built-in function!

df_CO["Edad"].std()

np.float64(18.65709106452142)

Takeaways

Takeaway Messages

• Visualize quantitative variables with histograms or densities.

• Summarize the center of a quantitative variable with mean or median.

• Describe the shape of a quantitative variable with skew.

• Summarize the spread of a quantitative variable with the variance or the standard deviation.