Visualizing and Comparing Categorical Variables

The story so far…

Getting and Prepping Data

df = pd.read_csv("https://datasci112.stanford.edu/data/titanic.csv")

df["pclass"] = df["pclass"].astype("category")
df["survived"] = df["survived"].astype("category")

Thinking About Variable Types

name	pclass	survived	sex	age	sibsp	parch	ticket	fare	cabin	embarked	boat	body	home.dest
Allen, Miss. Elisabeth Walton	1	1	female	29.0000	0	0	24160	211.3375	B5	S	2	NaN	St Louis, MO
Allison, Master. Hudson Trevor	1	1	male	0.9167	1	2	113781	151.5500	C22 C26	S	11	NaN	Montreal, PQ / Chesterville, ON
Allison, Miss. Helen Loraine	1	0	female	2.0000	1	2	113781	151.5500	C22 C26	S	NA	NaN	Montreal, PQ / Chesterville, ON
Allison, Mr. Hudson Joshua Creighton	1	0	male	30.0000	1	2	113781	151.5500	C22 C26	S	NA	135	Montreal, PQ / Chesterville, ON
Allison, Mrs. Hudson J C (Bessie Waldo Daniels)	1	0	female	25.0000	1	2	113781	151.5500	C22 C26	S	NA	NaN	Montreal, PQ / Chesterville, ON
Anderson, Mr. Harry	1	1	male	48.0000	0	0	19952	26.5500	E12	S	3	NaN	New York, NY

Accessing Rows and Columns

df.iloc[5,]

name         Anderson, Mr. Harry
pclass                         1
survived                       1
sex                         male
age                         48.0
sibsp                          0
parch                          0
ticket                     19952
fare                       26.55
cabin                        E12
embarked                       S
boat                           3
body                         NaN
home.dest           New York, NY
Name: 5, dtype: object

df["name"].head()

0                      Allen, Miss. Elisabeth Walton
1                     Allison, Master. Hudson Trevor
2                       Allison, Miss. Helen Loraine
3               Allison, Mr. Hudson Joshua Creighton
4    Allison, Mrs. Hudson J C (Bessie Waldo Daniels)
Name: name, dtype: object

Quick Summary of Quantitative Variables

df.describe()

               age        sibsp        parch         fare        body
count  1046.000000  1309.000000  1309.000000  1308.000000  121.000000
mean     29.881135     0.498854     0.385027    33.295479  160.809917
std      14.413500     1.041658     0.865560    51.758668   97.696922
min       0.166700     0.000000     0.000000     0.000000    1.000000
25%      21.000000     0.000000     0.000000     7.895800   72.000000
50%      28.000000     0.000000     0.000000    14.454200  155.000000
75%      39.000000     1.000000     0.000000    31.275000  256.000000
max      80.000000     8.000000     9.000000   512.329200  328.000000

Summarizing Categorical Variables

The list of percents for each category is called the distribution of the variable.

df["pclass"].value_counts()

pclass
3    709
1    323
2    277
Name: count, dtype: int64

df["pclass"].value_counts(normalize = True)

pclass
3    0.541635
1    0.246753
2    0.211612
Name: proportion, dtype: float64

Visualizing One Categorical Variable

The Grammar of Graphics

The grammar of graphics is a framework for creating data visualizations.

A visualization consists of:

• The aesthetic: Which variables are dictating which plot elements.

• The geometry: What shape of plot you are making.

• The theme: Other choices about the appearance.

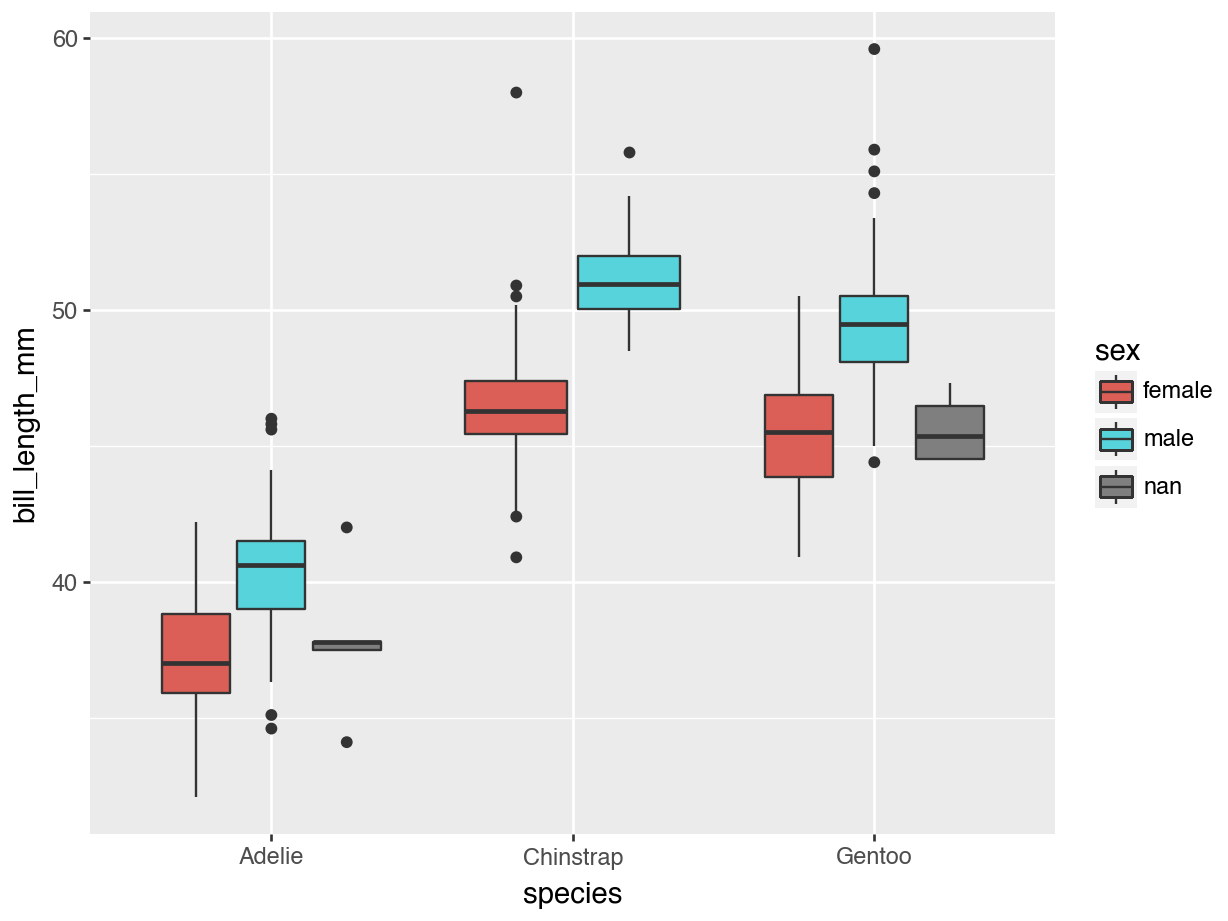
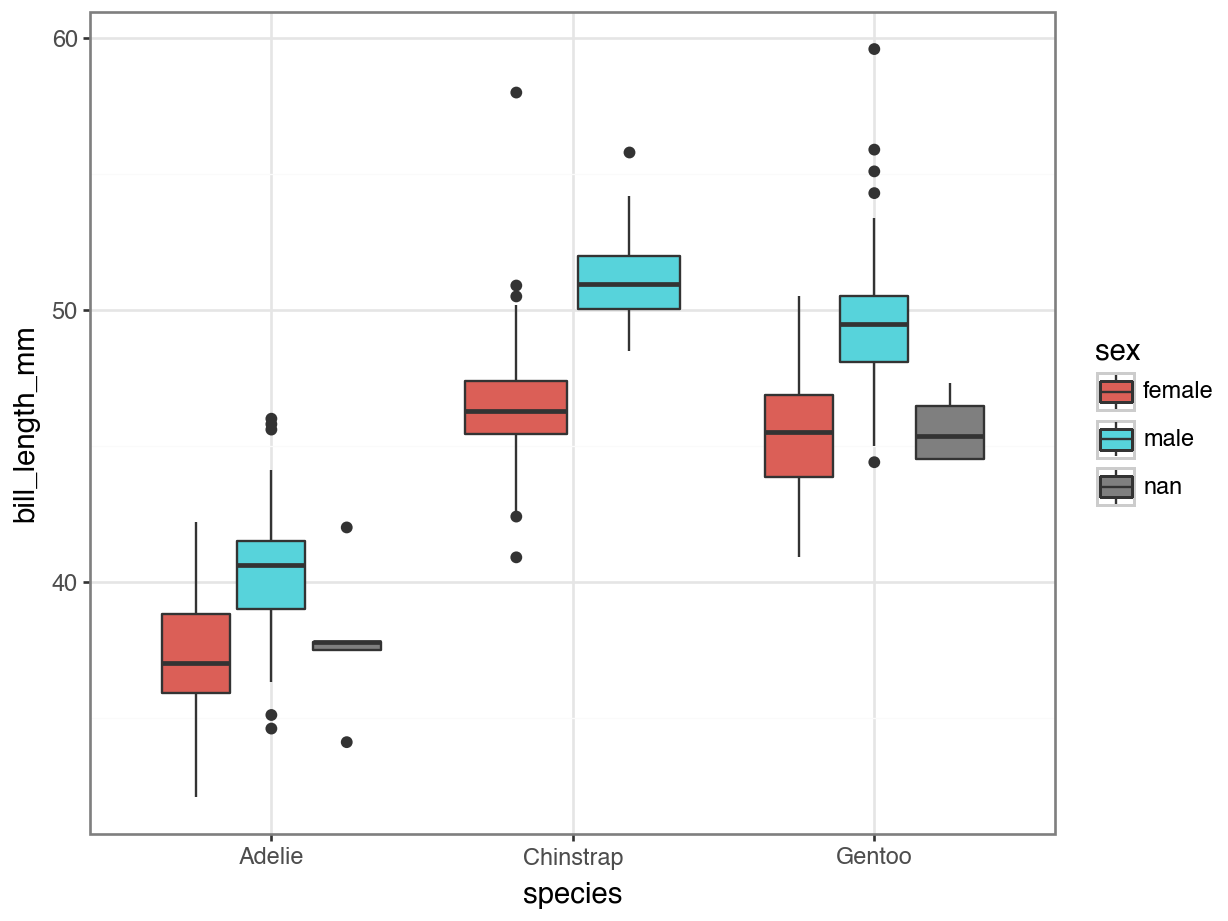
Example

import pandas as pd
from palmerpenguins import load_penguins
from plotnine import ggplot, geom_point, aes, geom_boxplot

penguins = load_penguins()

(
  ggplot(data = penguins, mapping = aes(x = "species", 
                                        y = "bill_length_mm", 
                                        fill = "sex")
        ) +
  geom_boxplot()
)

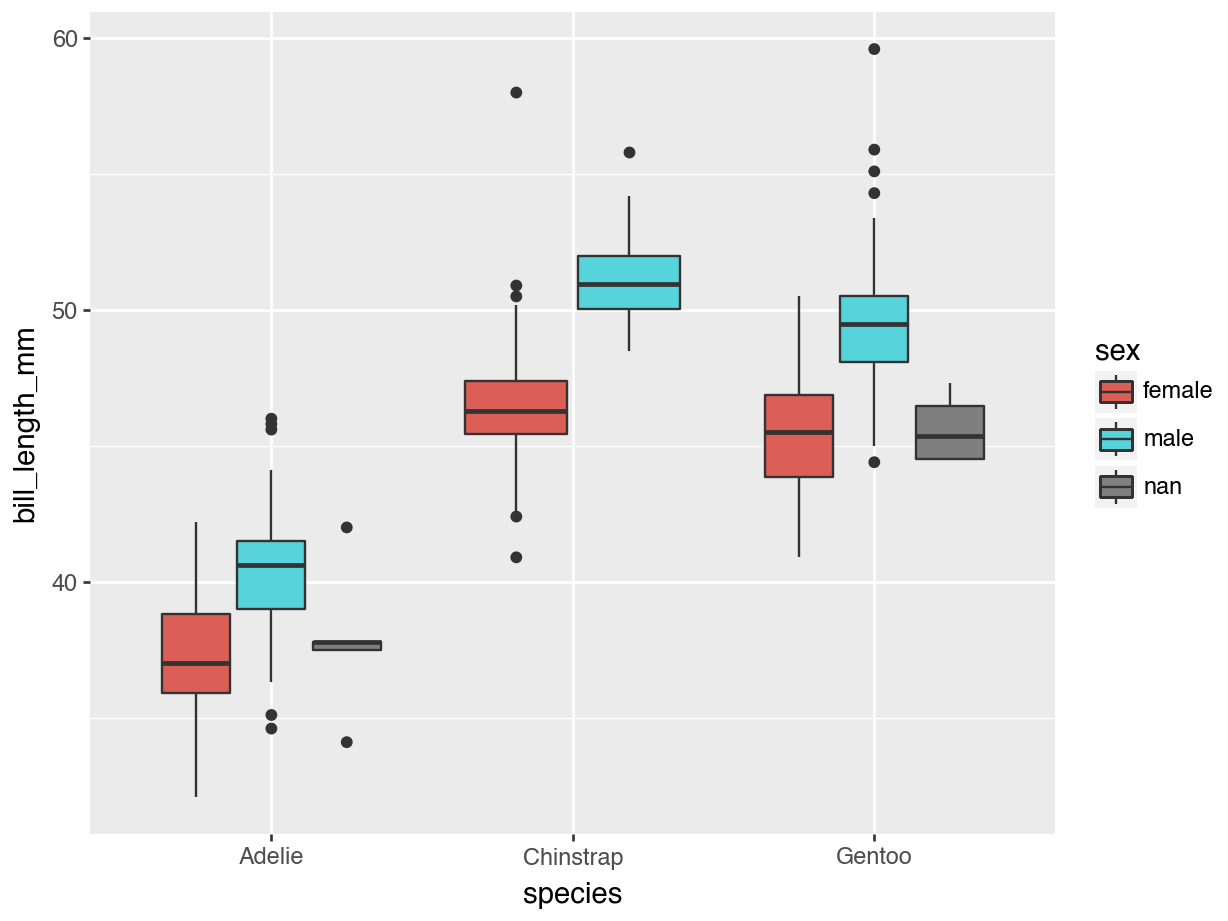
Aesthetics

Where are variables mapped to aspects of the plot?

Geometry

What shape(s) are used to represent the data / observations?

plotnine

The plotnine library implements the grammar of graphics in Python.

• The aes() function is the place to map variables to plot aesthetics.
  • x, y, and fill are three possible aesthetics that can be specified
• A variety of geom_XXX() functions allow for different plotting shapes (e.g. boxplot, histogram, etc.)
  • Aesthetics can differ based on the geom you choose!

Themes

(
  ggplot(data = penguins, mapping = aes(x = "species", 
                                        y = "bill_length_mm", 
                                        fill = "sex")
         ) + 
  geom_boxplot()
)

from plotnine import theme_bw

(
  ggplot(penguins, aes(x = "species", 
                       y = "bill_length_mm", 
                       fill = "sex")
                       ) + 
  geom_boxplot() + 
  theme_bw()
)

Check-In

What are the aesthetics and geometry in the cartoon plot below?

An XKCD comic

Bar Plots

To visualize the distribution of a categorical variable, we should use a bar plot.

from plotnine import *

(
  ggplot(data = df, mapping = aes(x = "pclass")) + 
  geom_bar() + 
  theme_bw()
)

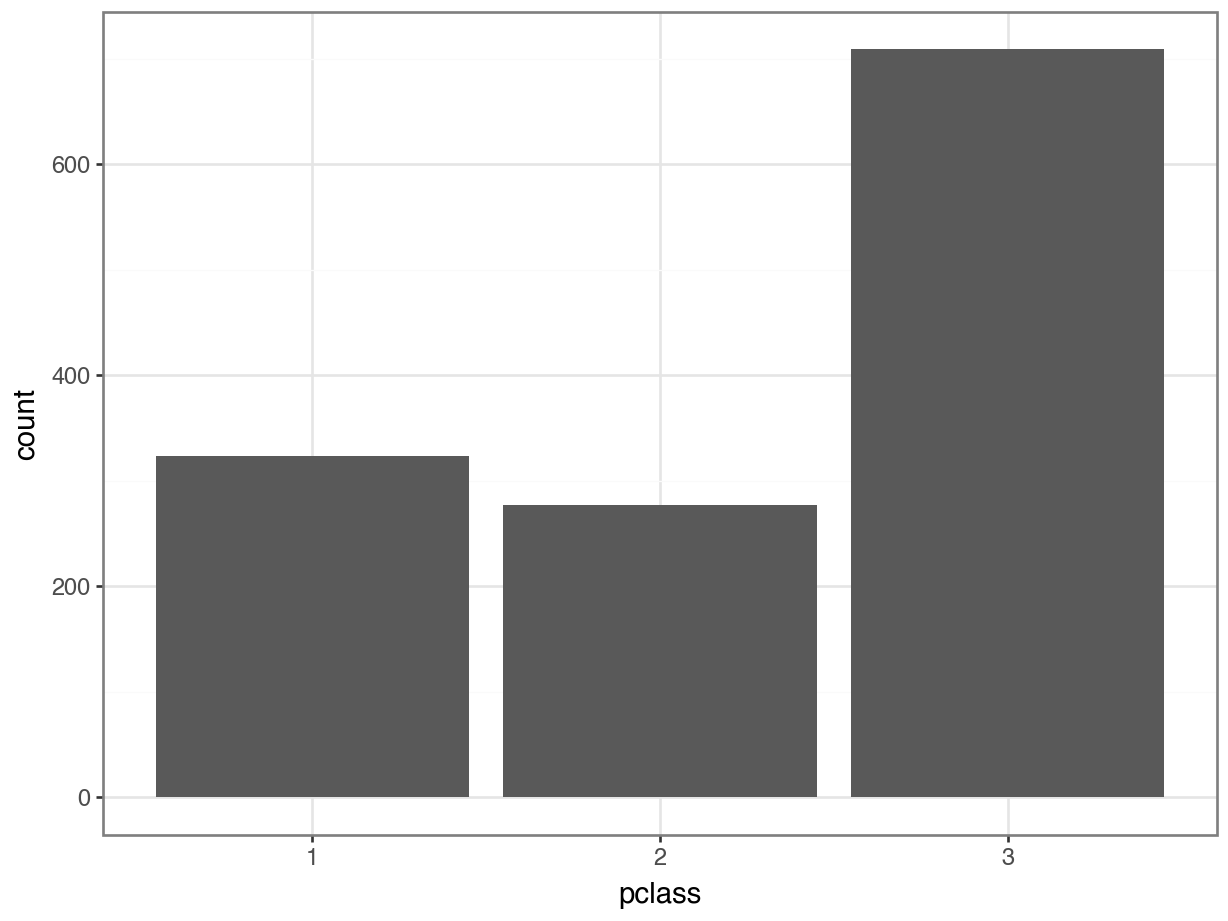
Calculating Percents

pclass_dist = (
  df['pclass']
  .value_counts(normalize = True)
  .reset_index()
  )
  
pclass_dist

  pclass  proportion
0      3    0.541635
1      1    0.246753
2      2    0.211612

Percents on Plots

(
  ggplot(data = pclass_dist, 
         mapping = aes(x = "pclass", y = "proportion")) + 
  geom_col() + ### notice this change to a column plot!
  theme_bw()
)

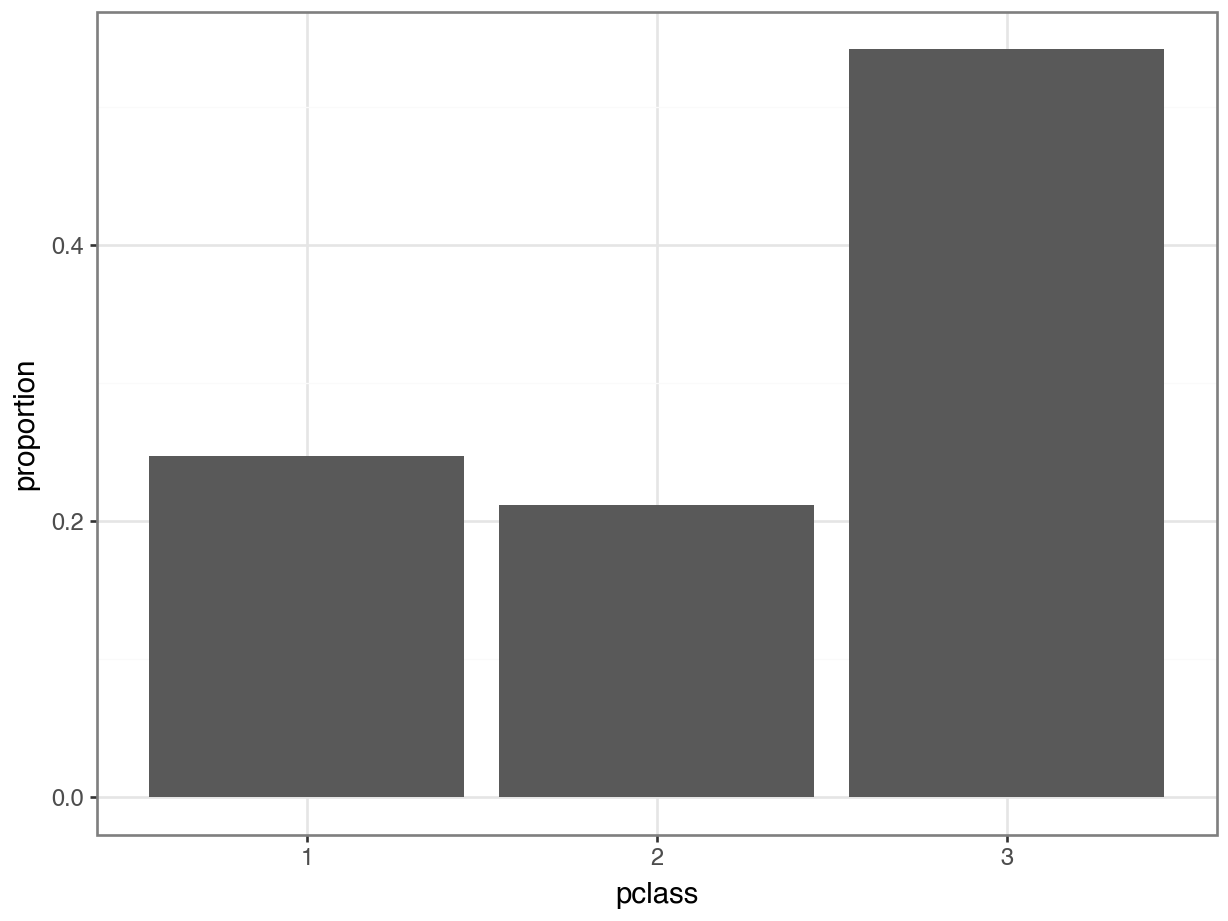
Tip

Technically, you could still use geom_bar(), but you would need to specify that you didn’t want it to use stat = "count" (the default). You’ve already calculated the proportions, so you would use geom_bar(stat = "identity").

Visualizing Two Categorical Variables

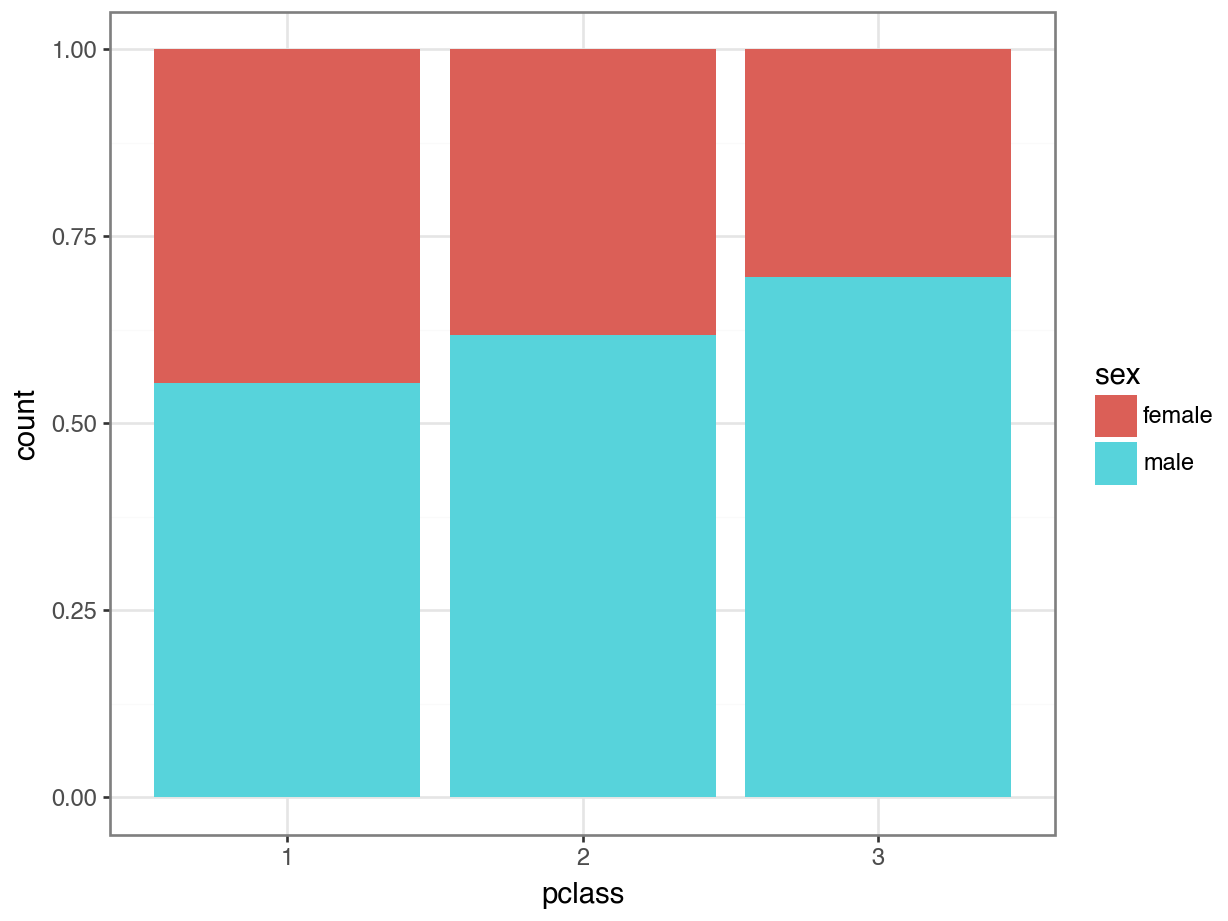
Option 1: Stacked Bar Plot

(
  ggplot(data = df, mapping = aes(x = "pclass", fill = "sex")) + 
  geom_bar(position = "stack") + 
  theme_bw()
)

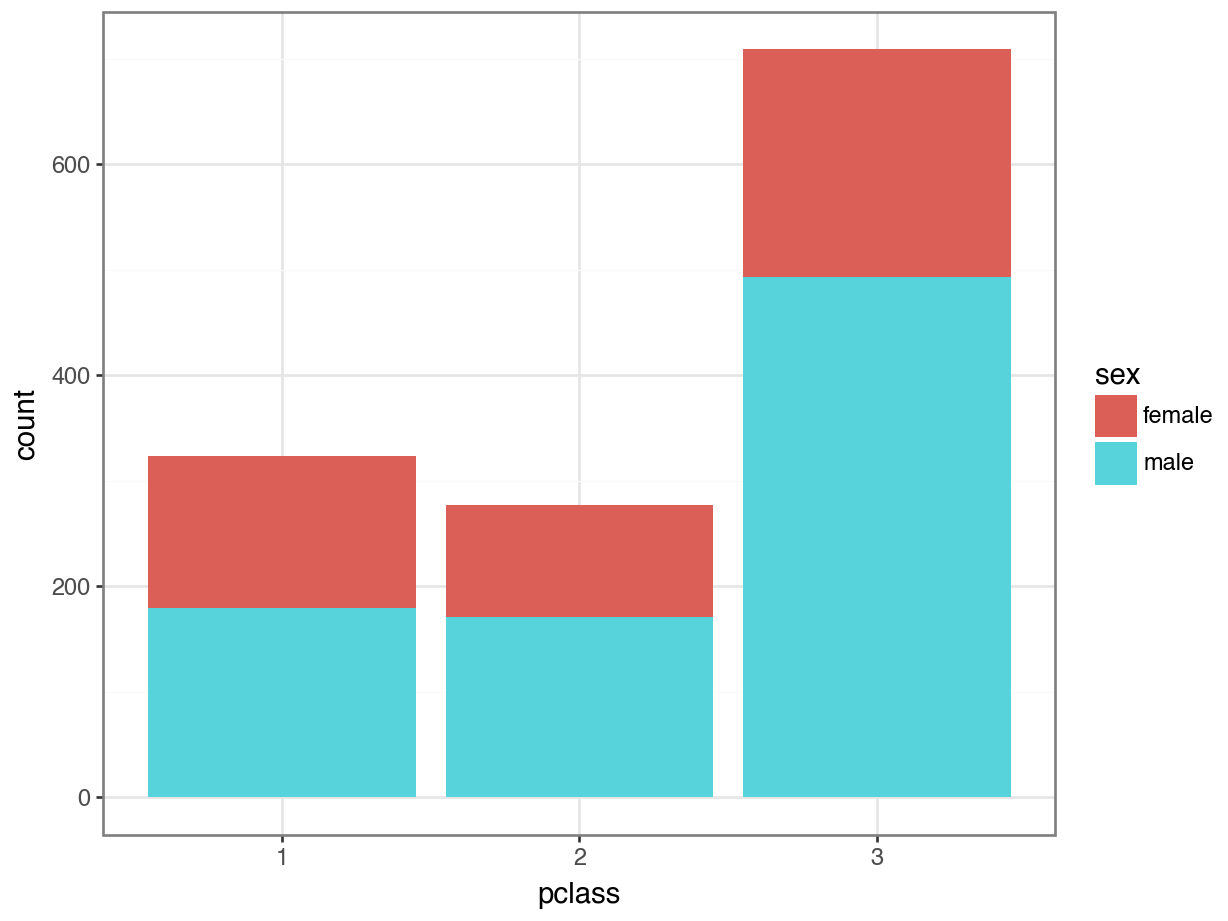
Option 1: Stacked Bar Plot

What are some pros and cons of the stacked bar plot?

Pros

• We can still see the total counts in each class
• We can easily compare the male counts in each class, since those bars are on the bottom.

Cons

• It is hard to compare the female counts, since those bars are stacked on top.
• It is hard to estimate the distributions.

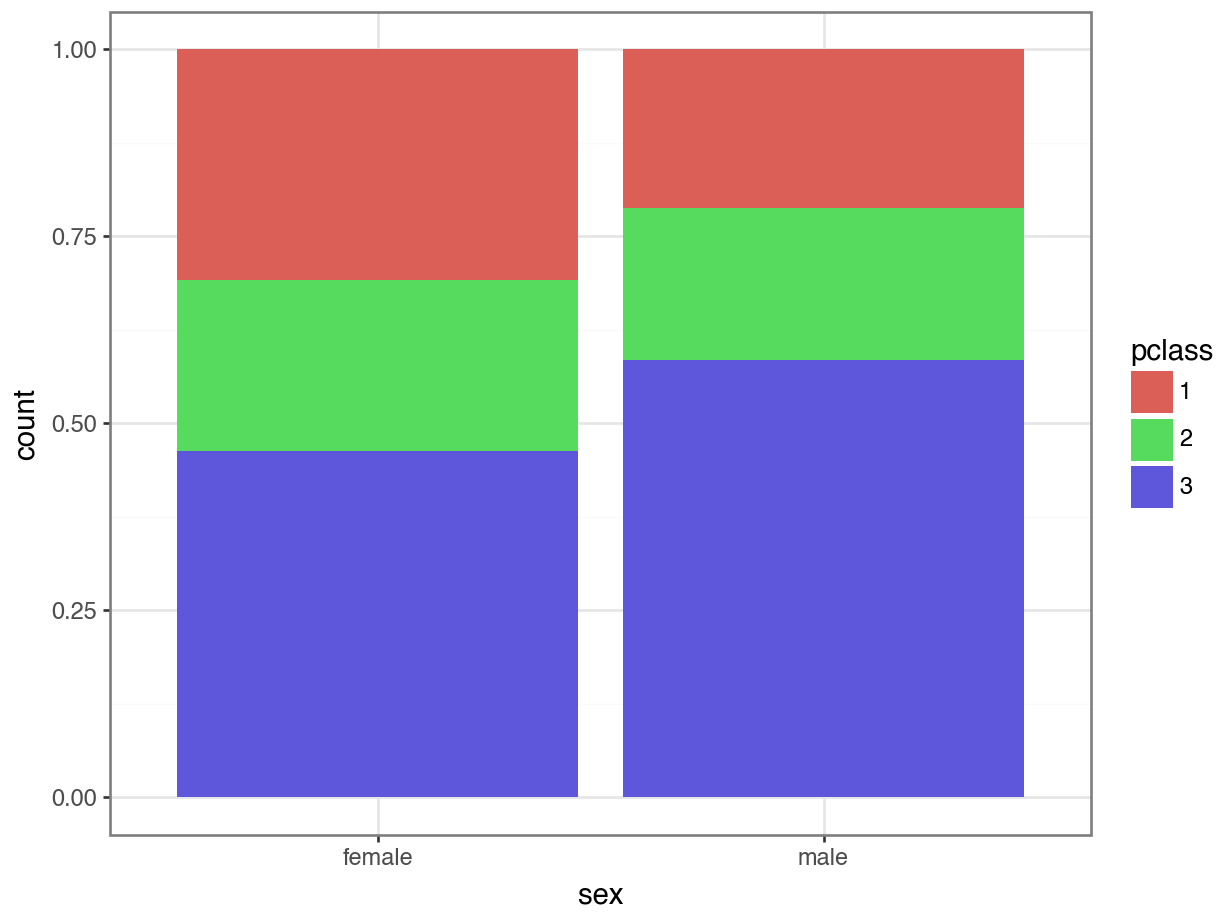
Option 2: Side-by-Side Bar Plot

(
  ggplot(data = df, mapping = aes(x = "pclass", fill = "sex")) + 
  geom_bar(position = "dodge") + 
  theme_bw()
)

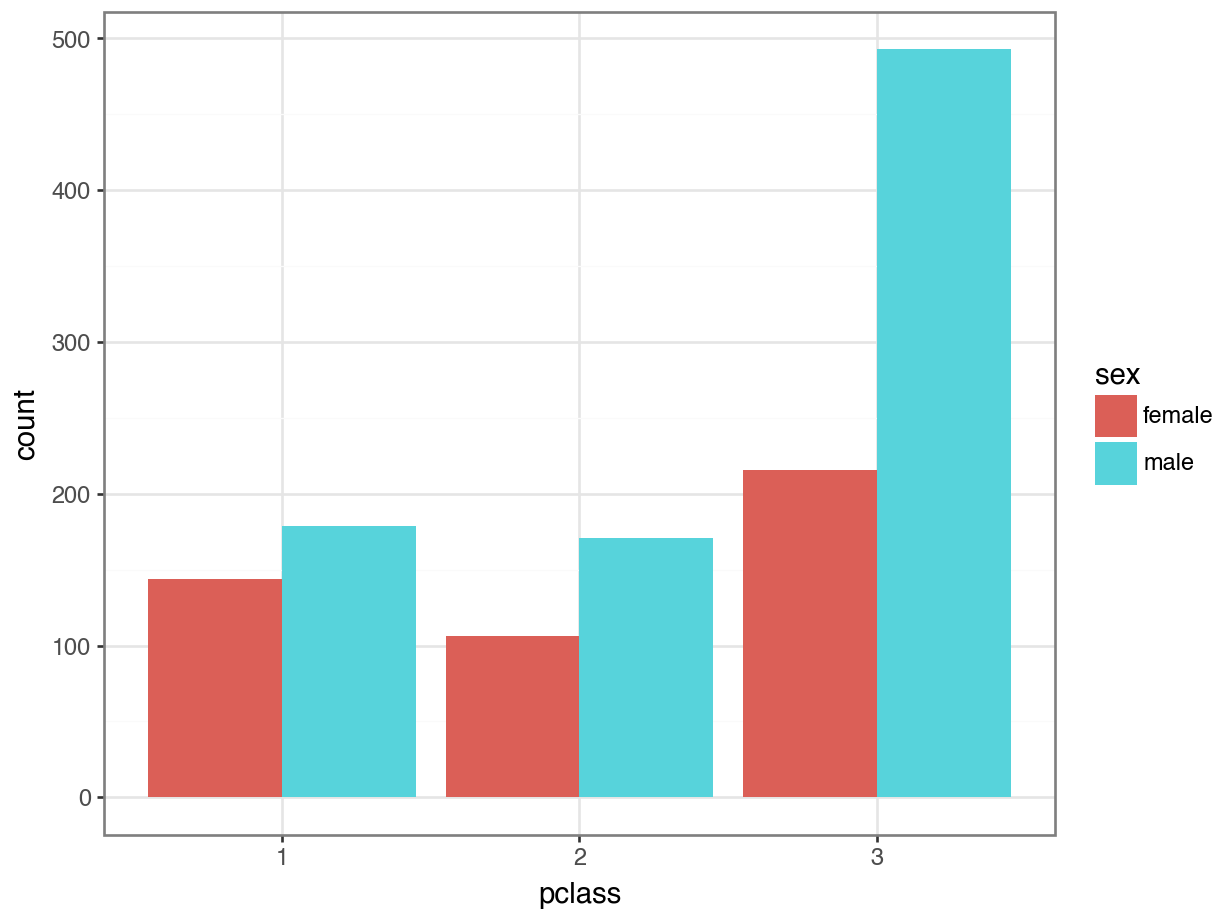
Option 2: Side-by-side Bar Plot

What are some pros and cons of the side-by-side bar plot?

Pros

• We can easily compare the female counts in each class.

• We can easily compare the male counts in each class.

• We can easily see counts of each within each class.

Cons

• It is hard to see total counts in each class.

• It is hard to estimate the distributions.

Option 3: Stacked Percentage Bar Plot

(
  ggplot(data = df, mapping = aes(x = "pclass", fill = "sex")) + 
  geom_bar(position = "fill") + 
  theme_bw()
)

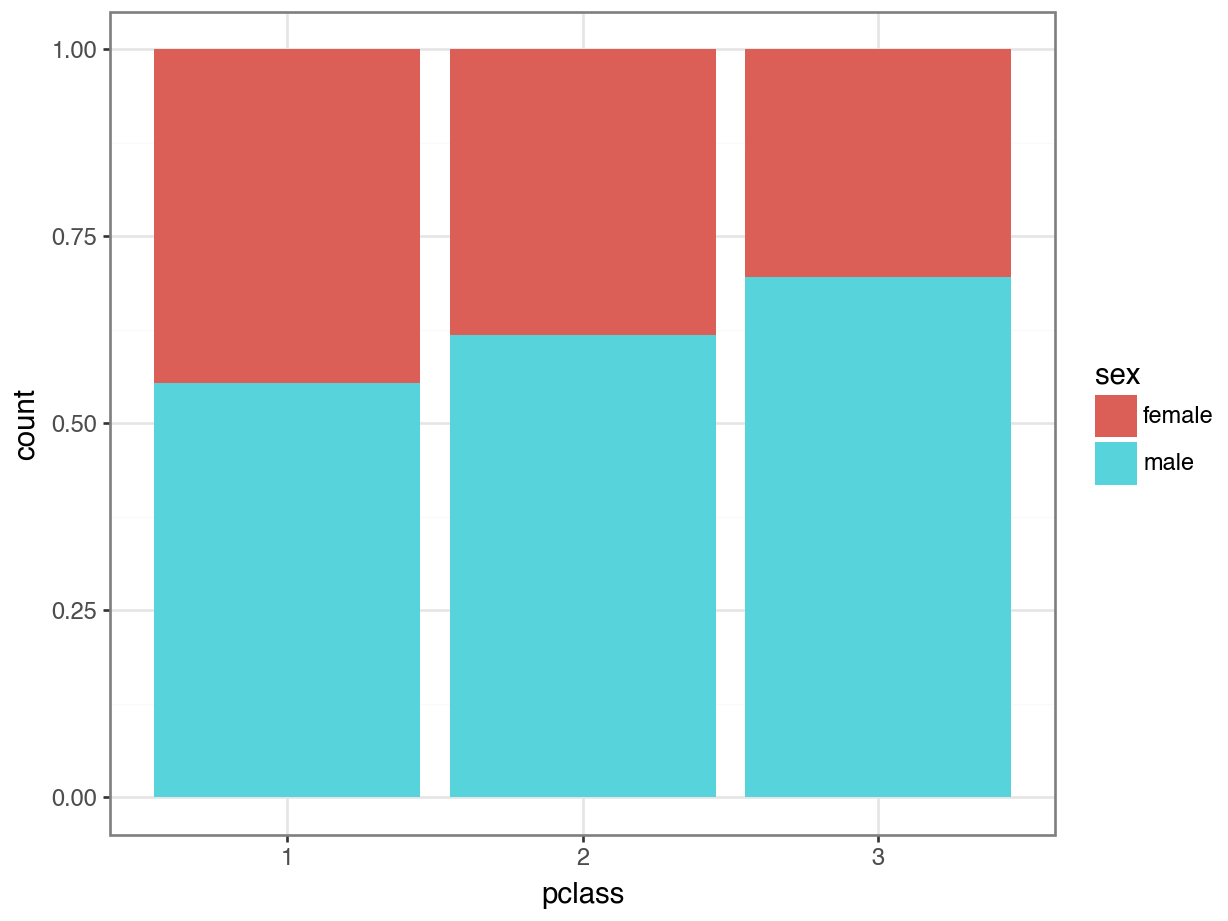
Option 3: Stacked Percentage Bar Plot

What are some pros and cons of the stacked percentage bar plot?

Pros

• This is the best way to compare sex balance across classes!

• This is the option I use the most, because it can answer “Are you more likely to find ______ in ______ ?” type questions.

Cons

• We can no longer see any counts!

Activity 1.2

Choose one of the plots from lecture so far and “upgrade” it.

You can do this by:

• Finding and using a different theme

• Using labs() to change the axis labels

• Trying different variables

• Trying a different geometries

• Using + scale_fill_manual() to change the colors being used

Tip

• You will need to use documentation of plotnine and online resources!

• Check out https://www.data-to-viz.com/ for ideas and example code.

• Ask GenAI questions like, “What do I add to a plotnine bar plot to change the colors?” (But of course, make sure you understand the code you use!)

Joint distributions

Two Categorical Variables

df[["pclass", "sex"]].value_counts()

pclass  sex   
3       male      493
        female    216
1       male      179
2       male      171
1       female    144
2       female    106
Name: count, dtype: int64

Two-way Table

(
  df[["pclass", "sex"]]
  .value_counts()
  .unstack()
  )

sex     female  male
pclass              
1          144   179
2          106   171
3          216   493

This is sometimes called a cross-tab or cross-tabulation.

Pivot Table

Essentially unstack() has pivoted the sex column from long format (where the values are included in one column) to wide format where each value has its own column.

Two-way Table - Percents

(
  df[["pclass", "sex"]]
  .value_counts(normalize = True)
  .unstack()
  )

sex       female      male
pclass                    
1       0.110008  0.136746
2       0.080978  0.130634
3       0.165011  0.376623

All of these values should sum to 1, aka, 100%!

Switching Variable Order

What cross-tabulation would you expect if we changed the order of the variables? In other words, what would happen if "sex" came first and "pclass" came second?

(
  df[["sex", "pclass"]]
  .value_counts(normalize = True)
  .unstack()
  )

pclass         1         2         3
sex                                 
female  0.110008  0.080978  0.165011
male    0.136746  0.130634  0.376623

Interpretation

We call this the joint distribution of the two variables.

sex       female      male
pclass                    
1       0.110008  0.136746
2       0.080978  0.130634
3       0.165011  0.376623

Of all the passengers on the Titanic, 11% were female passengers riding in first class.

• NOT “11% of all females on Titanic…”
• NOT “11% of all first class passengers…”

Conditional Distribution from Counts

We know that:

• 466 passengers identified as female

• Of those 466 passengers, 144 rode in first class

So:

• 144 / 466 = 31% of female identifying passengers rode in first class

Here we conditioned on the passenger being female, and then looked at the conditional distribution of pclass.

Conditional Distribution from Percentages

We know that:

• 35.5% of all passengers identified as female

• Of those 35.5% of passengers, 11% rode in first class

So:

• 0.11 / 0.355 = 31% of female identifying passengers rode in first class

Here we conditioned on the passenger being female, and then looked at the conditional distribution of pclass.

Swapping Variables

We know that:

• 323 passengers rode in first class

• Of those 323 passengers, 144 identified as female

So:

• 144 / 323 = 44.6% of first class passengers identified as female

Here we conditioned on the passenger being in first class, and then looked at the conditional distribution of sex.

Which one to condition on?

This depends on the research question you are trying to answer.

“What class did most female identifying passengers ride in?”

-> Of all female passengers, what is the conditional distribution of class?

“What was the gender breakdown of first class?”

-> Of all first class passengers, what is the conditional distribution of sex?

Calculating in Python

When we study two variables, we call the individual one-variable distributions the marginal distribution of that variable.

marginal_class = (
  df['pclass']
  .value_counts(normalize = True)
  )

marginal_class

pclass
3    0.541635
1    0.246753
2    0.211612
Name: proportion, dtype: float64

marginal_sex = (
  df['sex']
  .value_counts(normalize = True)
  )

marginal_sex

sex
male      0.644003
female    0.355997
Name: proportion, dtype: float64

Calculating in Python

We need to divide the joint distribution (e.g. “11% of passengers were first class female”) by the marginal distribution of the variable we want to condition on (e.g. 35.5% of passengers were female).

joint_class_sex = (
  df[["pclass", "sex"]]
  .value_counts(normalize = True)
  .unstack()
  )
  
joint_class_sex.divide(marginal_sex)

sex       female      male
pclass                    
1       0.309013  0.212337
2       0.227468  0.202847
3       0.463519  0.584816

Check-In

marginal_sex

sex
male      0.644003
female    0.355997
Name: proportion, dtype: float64

joint_class_sex

sex       female      male
pclass                    
1       0.110008  0.136746
2       0.080978  0.130634
3       0.165011  0.376623

joint_class_sex.divide(marginal_sex)

sex       female      male
pclass                    
1       0.309013  0.212337
2       0.227468  0.202847
3       0.463519  0.584816

How do you think divide() works?

Check-In

Should the rows or columns add up to 100%? Why?

sex       female      male
pclass                    
1       0.309013  0.212337
2       0.227468  0.202847
3       0.463519  0.584816

Conditional on Class

joint_class_sex = (
  df[["sex", "pclass"]]
  .value_counts(normalize = True)
  .unstack()
  )
  
joint_class_sex.divide(marginal_class)

pclass        1         2         3
sex                                
female  0.44582  0.382671  0.304654
male    0.55418  0.617329  0.695346

What if you get it backwards?

joint_class_sex = (
  df[["pclass", "sex"]]
  .value_counts(normalize = True)
  .unstack()
  )
  
joint_class_sex.divide(marginal_class)

         1   2   3  female  male
pclass                          
1      NaN NaN NaN     NaN   NaN
2      NaN NaN NaN     NaN   NaN
3      NaN NaN NaN     NaN   NaN

Which plot better answers the question:

“Did women tend to ride in first class more than men?”

(
  ggplot(df, aes(x = "pclass", fill = "sex")) + 
  geom_bar(position = "fill") + 
  theme_bw()
)

(
  ggplot(df, aes(x = "sex", fill = "pclass)) + 
  geom_bar(position = "fill") + 
  theme_bw()
)

Takeaways

Takeaways

• We use plotnine and the grammar of graphics to make visuals.

• For two categorical variables, we might use a stacked bar plot, a side-by-side bar plot, or a stacked percentage bar plot - depending on what we are trying to show.

• The joint distribution of two variables gives the percents in each subcategory.

• The marginal distribution of a variable is its individual distribution.

• The conditional distribution of a variable is its distribution among only one category of a different variable.

• We calculate the conditional distribution by dividing the joint by the marginal.